The Campbell Group is part of the Condensed Matter Theory section at the Physics Department of Boston University.  We currently conduct research in three areas: ultracold atomic gases, graphene devices, the functional renormalization group, and nonlinear dynamics.  Our broader interests include chaos, nonlinear phenomena, exotic ground states, strongly correlated electronic systems, and low-dimensional materials.

Ultracold atomic gases

My long-term interest in “intrinsic localized modes” (ILMs) (also known as “discrete breathers”) [1,2] has recently led to a study of their role in “avalanches” of Bose-Einstein Condensates (BEC) in (tilted) optical lattices in the semi-classical limit [3]. This, in turn, led to a further study of quantum effects beyond the semi-classical limit, using a global phase space (GPS) approach [4]. Currently, we are extending this GPS approach to the case where dissipation is present, with the surprising result that dissipation can actually enhance coherence and entanglement, effectively through the creation of stable ILMs in individual wells of the optical lattice [5].

Relevant papers:

1. David K. Campbell, Sergej Flach, and Yuri S. Kivshar (2004), Localizing Energy Through Nonlinearity and Discreteness
2. J. Dorignac, J. Zhou, and D. K. Campbell (2008), Discrete breathers in nonlinear Schrödinger hypercubic lattices with arbitrary power nonlinearity
3. H. Hennig, J. Dorignac and D. K. Campbell (2010), Transfer of Bose-Einstein condensates through discrete breathers in an optical lattice
4. H. Hennig, D. Witthaut and D. K. Campbell (2012), Global phase space of coherence and entanglement in a double-well Bose-Einstein condensate
5. T. Pudlik, H. Hennig, D. Witthaut and D. K. Campbell (2013),  Dynamics of entanglement in a dissipative Bose–Hubbard dimer

Graphene and other 2D electronic materials

The isolation and characterization of graphene as an atomically thin monolayer of pure carbon by Novoselov, Geim, and their collaborators in 2004 produced an avalanche of interest across the condensed matter physics community, from theorists to experimentalists to applied materials scientists and device builders. Working with a number of collaborators, we have studied several different aspects of this exceptional material. For monolayer graphene, we developed a simple model for the phonon spectrum [1] and studied how the monolayer adhered to a patterned substrate [2]. For bilayer graphene, we explored the electronic compressibility [3] and the effects of electron-electron interactions [4]. Very recent studies include modeling the effects on electronic transport of the pseudomagnetic fields produced by non-uniform strain in graphene [5] and exploring a novel non-equilibrium steady state mechanism for inducing an effective gap in graphene [6]. We are currently extending our transport calculations to graphene “bubbles” of arbitrary shape, generated, for example, by applying gas pressure to graphene stretched over a nanocavity.

Graphene, while of enormous recent theoretical and experimental interest, is limited in its application in electronics by its gaplessness. Hence we are extending our research to other two-dimensional materials, and in particular to the semiconducting transition metal dichalcogenides (TMDCs), many of which have direct bandgaps on the order of 1-2 eV in monolayer form. We plan to apply the same approaches to these materials as used in our studies of graphene [5].

Relevant papers:

1. S. Viola-Kusminsky, D. K. Campbell, and A. H. Castro Neto (2009), Lenosky’s energy and the phonon dispersion of graphene
2. S. Viola Kusminsky, D. K. Campbell, A. H. Castro Neto, F. Guinea (2011), 2D Membrane on top of a patterned substrate: the case of graphene
3. S. Viola-Kusminsky, Johan Nilsson, D. K. Campbell, and A. H. Castro Neto (2007), Electronic Compressibility of a graphene bilayer
4. S. Viola-Kusminsky, D. K. Campbell, and A. H. Castro Neto (2009), Electron-electron interactions in graphene bilayers
5. Z. Qi, D. A. Bahamon, V. M. Pereira, H. S. Park, D. K. Campbell and A. H. Castro Neto (2013), Resonant tunneling in graphene pseudomagnetic quantum dots
6. Thomas Iadecola. David Campbell, Claudio Chamon, Chang-Yu Hou, Roman Jackiw, So-Young Pi, and Silvia Viola Kusminskiy (2013), Materials Design from Nonequilibrium Steady States: Driven Graphene as a Tunable Semiconductor with Topological Properties

Functional Renormalization Group

For nearly a decade, working with several different collaborators, we have applied variants of the functional renormalization group (FRG) to a wide range of models for novel, strongly correlated electronic systems. Examples have included superconductors in the strong coupling limit [1, 2, 3], the half-filled 1D extended Hubbard model [4], the two-leg Holstein-Hubbard ladder [5], the effects of dynamical phonons (retardation) on the half-filled 1D Holstein-Hubbard model [6], the validity of the Tomonga-Luttinger liquid relations for the 1D Holstein model [7], and the existence of dominant superconducting fluctuations in the 1D extended Hubbard-extended Holstein model [8]. Our most recent work in this area extends the FRG approach to the case of a mixture of two ultracold Fermionic atoms in a two-dimensional square optical lattice and predicts the existence of a novel d_xy number density wave state for certain ranges of the parameters in the theory [9].

Relevant papers:

1. S. W. Tsai, A.H.C. Neto, R. Shankar, and D. K. Campbell (2005), Renormalization-group approach to strong-coupled superconductors
2. S. W. Tsai, A.H.C. Neto, R. Shankar, and D. K. Campbell (2006), Strong coupling superconductivity via an asymptotically exact renormalization-group framework
3. S. W. Tsai, A.H.C. Neto, R. Shankar, and D. K. Campbell (2006), Renormalization-group approach to superconductivity: from weak to strong electron-phonon coupling
4. K. M. Tam, S. W. Tsai, and D. K. Campbell (2006), Functional renormalization group analysis of the half-filled one-dimensional extended Hubbard model
5. Ka-Ming Tam, S.-W. Tsai, D. K. Campbell, and A.H. Castro Neto (2007), Phase Diagram of the Holstein-Hubbard Two-Leg Ladder
6. Ka-Ming Tam, S.-W. Tsai, D. K. Campbell, and A. H. Castro Neto (2007), Retardation effects in the Holstein-Hubbard chain at half-filling
7. Ka-Ming Tam, S.-W. Tsai, and D. K. Campbell (2011), Validity of the Tomonaga-Luttinger Liquid relations for the one-dimensional Holstein model
8. Ka-Ming Tam, Shan-Wen Tsai, and David K. Campbell (2013) Dominant superconducting fluctuations in the 1D extended Holstein-extended Hubbard model
9. Chen-Yen Lai, Wen-Min Huang, David K. Campbell, and Shan-Wen Tsai, d_xy-density wave in fermion-fermion cold atom mixtures

Shortcuts to Adiabaticity

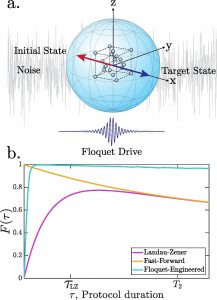
Adiabatic evolution is a common strategy for manipulating quantum states and has been employed in diverse fields such as quantum simulation, computation and annealing. However, adiabatic evolution is inherently slow and therefore susceptible to decoherence. Existing  methods for speeding up adiabatic evolution require complex many-body operators or are difficult to construct for multi-level systems. We have been working on methods to construct driving protocols that involve local or quasi-local operators.

• Using the tools of Floquet engineering, we design a scheme for high-fidelity quantum state manipulation, utilizing only the interactions available in the original Hamiltonian. Compared to the conventional fast-forward protocol, our Floquet-engineered protocol is more robust to external noise acting on the qubit. Our protocols were implemented in experiment done by our collaborators in Prof. Alex Sushkov’s lab. For details, check out our paper [1]

• Counter-diabatic (CD) Hamiltonian [2] helps in achieving transitionless evolution at arbitrary velocities by adding additional velocity-dependent counter terms to the Hamiltonian. However, CD Hamiltonian doesn’t exist in thermodynamic limit for chaotic systems. The question, which we are working on, is how can we define an approximate CD Hamiltonian for such systems?

Relevant papers:

1. E. Boyers, M. Pandey, D.K. Campbell, A. Polkovnikov, D. Sels and A.O. Sushkov, ( 2018) Floquet-engineered quantum state manipulation in a noisy qubit
2.  M. Kolodrubetz, D. Sels, P. Mehta, and A. Polkovnikov, (2017) Geometry and non-adiabatic response in quantum and classical systems.

Fermi-Pasta-Ulam-Tsingou Recurrences

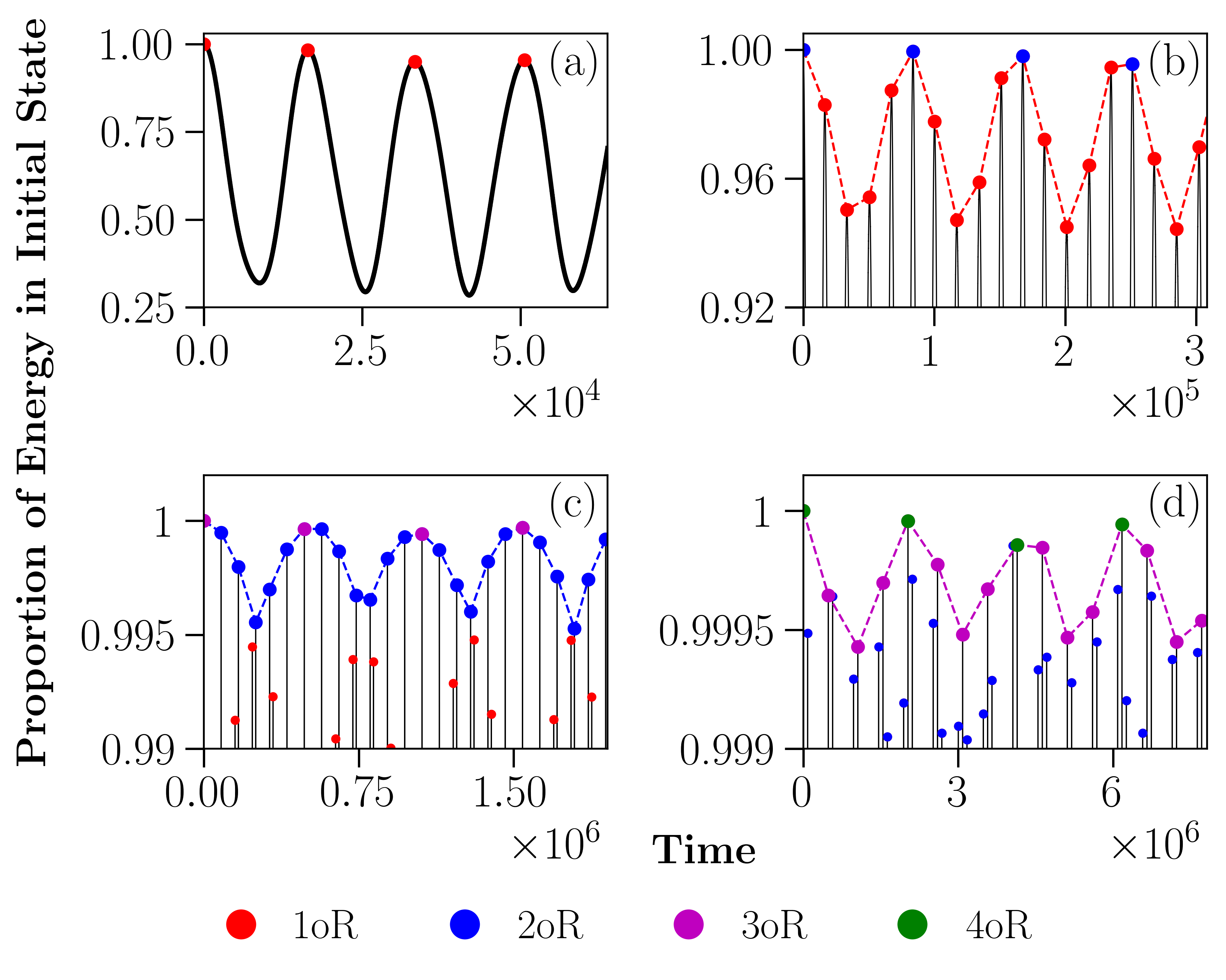Fermi-Pasta-Ulam-Tsingou (FPUT) recurrences have raised many questions regarding how FPUT models actually approach equilibrium [1]. Alongside FPUT recurrences are the super-recurrences which amount to a periodic modulation of the FPUT recurrence, where an even greater amount of energy is returned to the initial state. These complex behaviors are defining features of the nonequilibrium dynamics exhibited in the models’ metastable state. We have studied recurrences which include the original FPUT recurrences and super-recurrences, but also higher-order recurrences (HoRs) like super-super-recurrences. We have worked on understanding HoRs existence and periods as functions of energy and how their breakdown mechanisms relate to thermalization [2].

Relevant papers:

1. David K. Campbell and Phillip Rosenau (2005), Introduction: The Fermi-Pasta-Ulam problem – The first fifty years .
2. Salvatore D. Pace and David K. Campbell (2019), Behavior and Breakdown of Higher-Order Fermi-Pasta-Ulam-Tsingou Recurrences.