This graduate level text, written in collaboration with Paul Krapivsky
and Eli Ben-Naim was published by Cambridge University Press in December
2011.
Table of Contents and
Preface. Current List of
Errata.
 |
This graduate level text, written in collaboration with Paul Krapivsky
and Eli Ben-Naim was published by Cambridge University Press in December
2011. |

|
This book was published by Cambridge University Press in 2001. The cover illustrates first-passage in a finite interval where death awaits at one boundary and a restaurant date awaits at the other. Table of contents and preface. Current list of errata. Short list of exercises. Reviews of the book: by Alan Bray in Journal of Statistical Physics, February 2002. by Robert Dorfman in American Journal of Physics, November 2002. by Paolo Laureti, in Econophysics Forum, November 2002. |
|
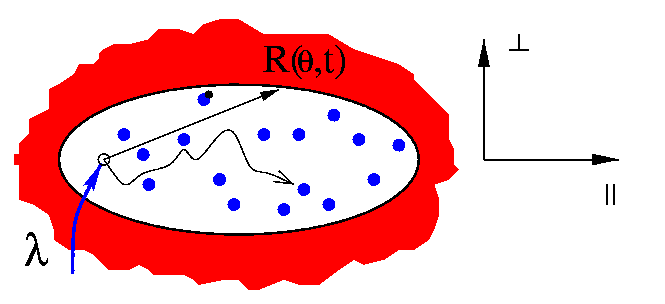
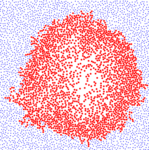
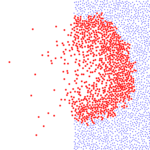
A single moving particle collides with one of the stationary particles in an
infinite zero-temperature gas of elastic particles at rest. The result
(left) is a collision cascade that propagates spherically outward. The
number of moving particles (red) at time t and the number collisions up to
time t grow as tξ and tη, with
ξ=2d/(d+2), η=2(d+1)/(d+2), and d the spatial dimension. These
growth laws are the same as those from a hydrodynamic theory for the shock
wave emanating from an explosion. For a particle incident on a static gas
that fills the half-space x>0 (right), the resulting backsplatter, or "break
shot" on an infinite pool table, ultimately contains almost all the initial
energy. For details, see
Exciting Hard Spheres, T. Antal,
P. L. Krapivsky, and S. Redner, Phys. Rev. E 78, 030301
(2008).
|

|
A typical metastable of the three-dimensional Ising model on a finite cube
with periodic boundary conditions in all directions. One phase of the spins
are represented as blue unit-size cubic blocks. This spin cluster has a
sponge-like topology so that there are no convex corners. The red blocks
denote "blinker" spins which can flip indefinitely with no energy cost. For
more information, see Freezing in Ising
Ferromagnets, V. Spirin, P. L. Krapivsky, and
S. Redner, Phys. Rev. E 65, 016119 (2001)
Zero-Temperature Freezing in
Three-Dimensional Kinetic Ising Model, J. Olejarz, P. L. Krapivsky, and
S. Redner, Phys. Rev. E 83, 030104(R) (2011), and
Zero-Temperature Relaxation of
Three-Dimensional Ising Ferromagnets, J. Olejarz, P. L. Krapivsky, and
S. Redner, Phys. Rev. E 83, 051104 (2011).
|

|
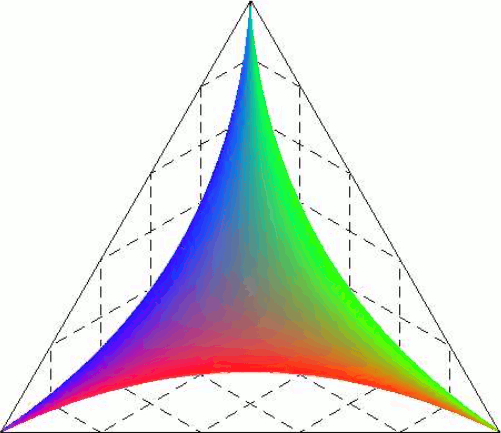
This interface is the result of depositing unit cubes inside a corner that
represents the positive octant of 3-space. The resulting growing interface
approaches a deterministic limiting shape in the long-time limit. The figure
on the left shows the result of a simulation of the interface at t=140, and
the right shows our theoretical prediction for the limiting shape that is
based on on the generalizing the corresponding interface in two dimensions to
three dimensions by accounting for the full symmetries of the system. For
more information, see
Growth Inside a Corner: The Limiting
Interface Shape, J. Olejarz, P. L. Krapivsky, S. Redner, and K. Mallick,
Phys. Rev. Lett. 108, 016102 (2012).
|




|
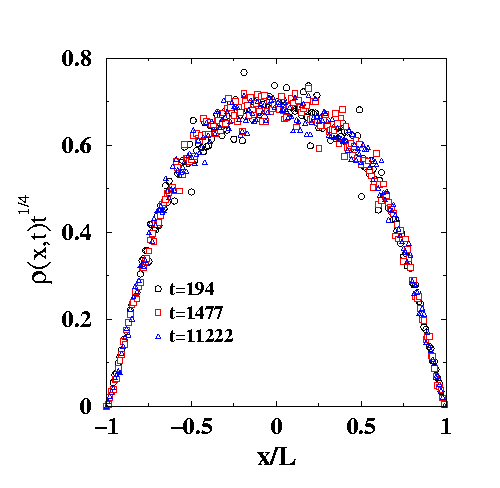
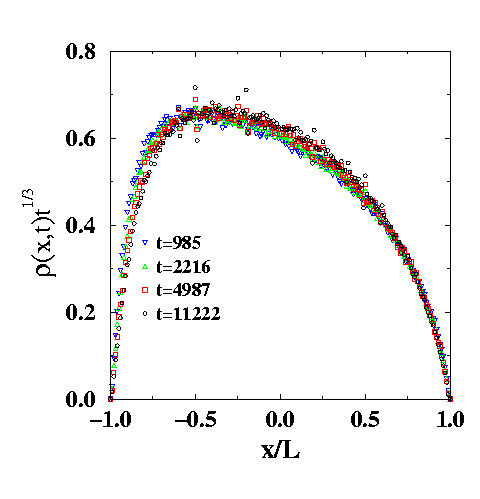
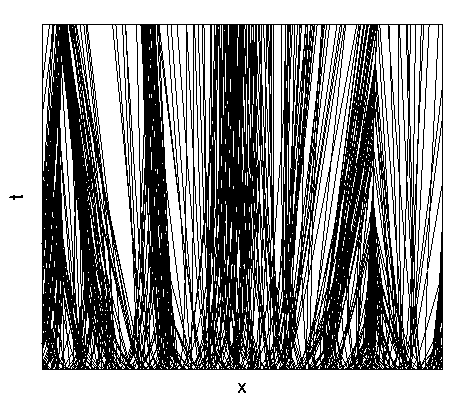
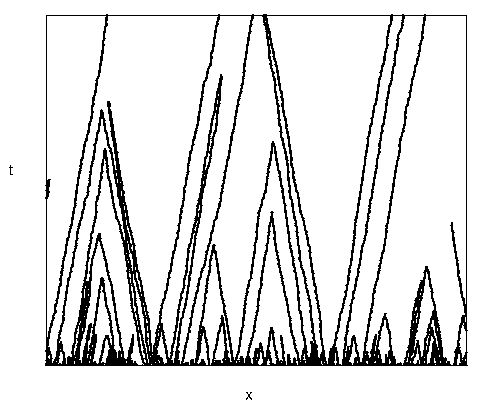
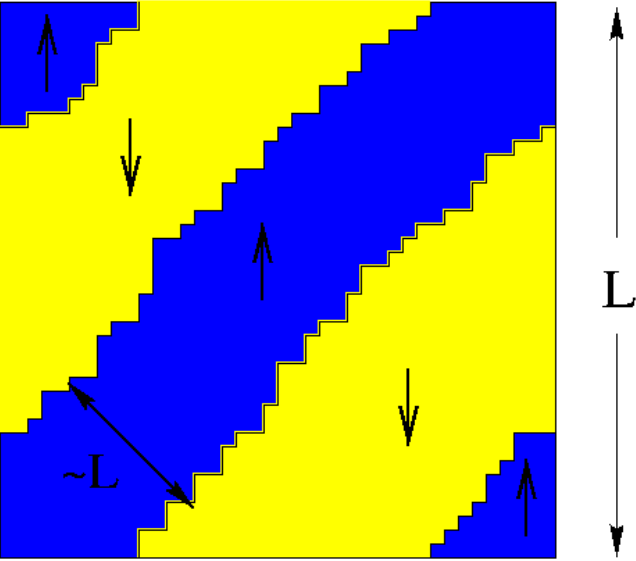
Long-lived "diagonal stripe" configuration on the square lattice with periodic boundary conditions. This configuration corresponds to a stripe that winds once around the torus equatorially and once toroidally, and arises in roughly 5% of all configurations. This diagonal stripe eventually and always reaches the ground state in a time that scales as L3.5. For details see Fate of Zero-Temperature Ising Ferromagnets, V. Spirin, P. L. Krapivsky, and S. Redner, Phys. Rev. E 63, 036118 (2001); and Freezing in Ising Ferromagnets, V. Spirin, P. L. Krapivsky, and S. Redner, Phys. Rev. E; 65, 016119 (2001). |
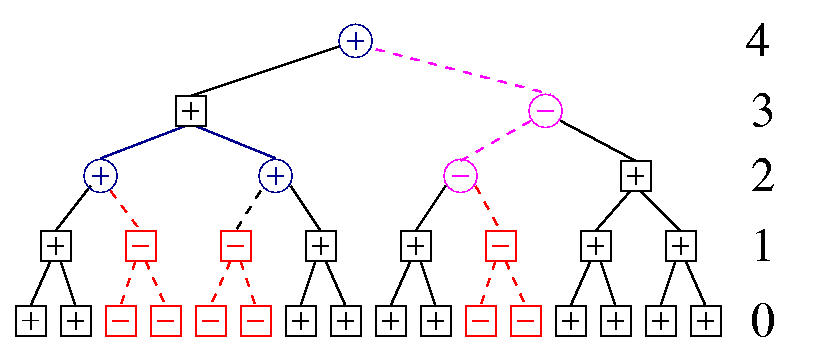 |
A typical metastable state of the homogeneous ferromagnetic Ising model with Glauber dynamics on the 3-coordinated Cayley tree. At zero temperature these metastable states are actually stable. Shown are the first 4 levels of the tree. Spins in squares have their state uniquely determined by the states of the two "daughter" spins (black for + spins, red for - spins). Spins in circles are determined by the spin state of their parent (blue for + spins, magenta for - spins). For details, see Freezing in Ising Ferromagnets, V. Spirin, P. L. Krapivsky, and S. Redner, Phys. Rev. E; 65, 016119 (2001). |
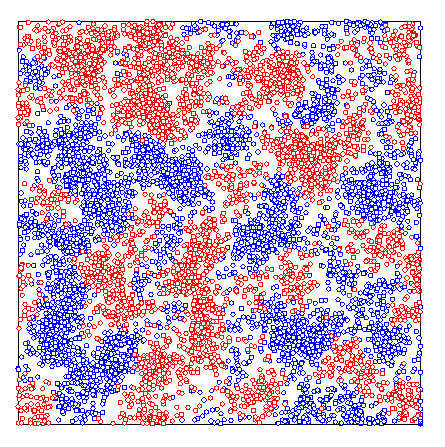
How can one characterize social networks with both friendly and unfriendly relations? A crucial concept is that of social balance, where each relationship triad contains an even number of friendly links. Such a triad fulfils the adage:
|
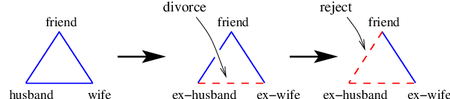
How do social networks evolve when both friendly and unfriendly relations exist? A familiar example is attempting to remain friendly with a married couple that gets divorced. It can be difficult to remain friendly with both former spouses if they dislike each other and the simplest solution may be to remain friends with only one of the former spouses. That is, change the sense of a link to eliminate imbalanced triads --- those that contain 1 or 3 unfriendly links. |

|
A more compelling example is the evolution of relations among the protagonists of World War I. These relationship changes gradually led to a reorganization of alliances between European nations into a socially balanced state. While social balance is a natural outcome, it is not necessarily a good one! |