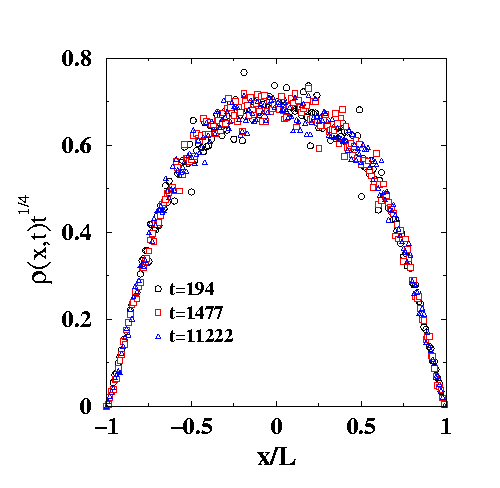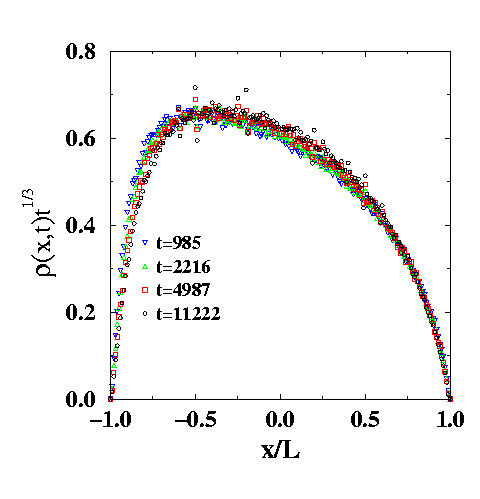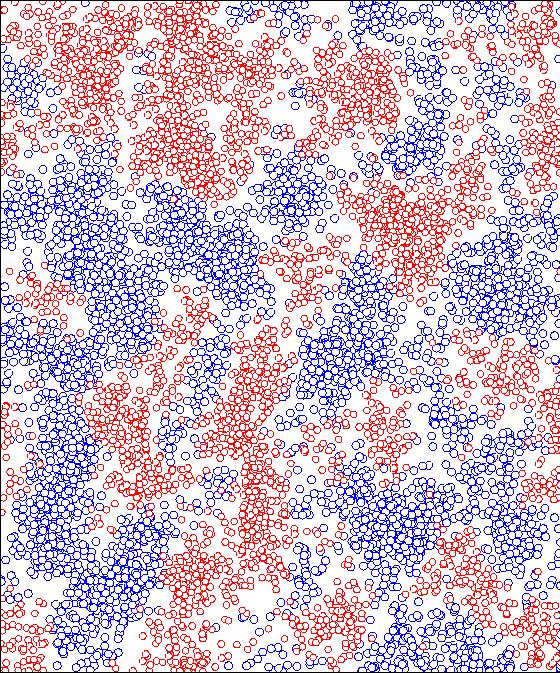
Here is a snapshot of a simulation of the diffusion-limited reaction A+B--->0 in two dimensions. The two species are indicated by the different colors. Note the existence of three length scales to describe the spatial distribution of reactants: (a) the typical distance between individual reactants, which grows with time as t^1/4; (ii) the typical domain size, which grows as t^1/2; and (iii) the "gap" distance between domains, which grows at t^1/3. The latter is the white space between domains and it is perhaps best visualized by squinting at the picture.

For details, see ``Spatial Organization in the Two-Species Annihilation Reaction A+B--->0'', Phys. Rev. Lett. 66, 2168, (1991); ``Spatial Structure in Diffusion-Limited Two-Species Annihilation'', Phys. Rev. A 46, 3132, (1992).

Here is the "microcanonical" density profile of reactants in one dimension when particles move by isotropic diffusion. This is defined by taking each domain and stretching or shrinking its length so that it lies between [-1,1], and then superposing the resulting density profiles. These profiles exhibit excellent data collapse when they are rescaled by a factor t^1/4.

Microcanonical density profile in one dimension when all particles move by driven diffusion. That is, all particles have the same overall drift superimposed on the diffusion. Naively, one would expect that this drift would have no effect on the density profile at large times. However, the drift is asymptotically relevant. Surprisingly, the density decays as t^-1/3 in one dimension, in contrast to the t^-1/4 decay in the absence of drift. Moreover, there is a long-time asymmetry in the density profile, as well as small deviations from scaling when the profiles are all rescaled by a factor of t^1/3.

For details, see ``Kinetics of A+B--->0 with Driven Diffusive Motion'', I. Ispolatov, P. L. Krapivsky, and S. Redner, Phys. Rev. E. 52, 2540 (1995).

Schematic illustration of the A+B--->0 dissolution process. Reactive A particles (filled circles) are continuously injected at rate lambda at a single point (open circle) and gradually opens up an elliptical dissolved region. Each particle undergoes biased diffusive motion with bias in the parallel direction. When a particle reaches the boundary of the dissolved region, a unit of the host B material and the particle both disappear via the reaction A+B--->0. For this geometry the length of the dissolved region grow as t^2/3 while the width grows as t^1/3.