

Next: About this document ...
Exercises to Accompany
A Guide to First-Passage Processes
This is a modest list of exercises to accompany ``A Guide to First-Passage
Processes'' and was last updated on December 8, 2002. I am indebted to
Prof. R. Dorfman for the suggestion to compile some exercises.
Chapter 1:
- Determine the asymptotic probability distribution for a random walk in
one dimension when the initial probability distribution is
broad. For example,
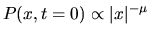 , with
, with 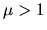 for
for 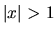 .
.
- Determine the asymptotic probability distribution for a one-dimensional
random walk that hops 2 lattice spacings to the right with
probability
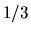 or hops 1 lattice spacing to the left with
probability
or hops 1 lattice spacing to the left with
probability 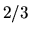 . Use the techniques of section 1.3.
. Use the techniques of section 1.3.
Chapter 2:
- Consider a diffusing particle in the interval
![$[0,L]$](img6.gif) that is initially
placed at
that is initially
placed at 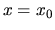 . There is a drift velocity
. There is a drift velocity 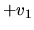 for
for
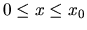 and a drift velocity
and a drift velocity 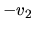 for
for
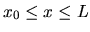 .
Compute the eventual exit probabilities to each end of the
interval. Compute the mean first-passage time to each end.
.
Compute the eventual exit probabilities to each end of the
interval. Compute the mean first-passage time to each end.
- Consider a diffusing particle that is initially located at the junction
of three line segments of lengths
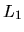 ,
, 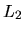 , and
, and 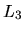 , with
, with
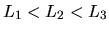 . The particle freely diffuses in each segment, but when the
end of a segment is reached the particle is absorbed. What is the
probability that the particle is eventually absorbed at the end of the
. The particle freely diffuses in each segment, but when the
end of a segment is reached the particle is absorbed. What is the
probability that the particle is eventually absorbed at the end of the
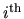 segment? What is the average time for the particle to be
absorbed at one of the endpoints? (That is, the identity of the absorbing
segment is unspecified when absorption occurs.) What is the average time
for the particle to be absorbed at the end of the
segment? What is the average time for the particle to be
absorbed at one of the endpoints? (That is, the identity of the absorbing
segment is unspecified when absorption occurs.) What is the average time
for the particle to be absorbed at the end of the 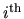 segment?
(That is, the identity of the absorbing segment is specified when
absorption occurs.)
segment?
(That is, the identity of the absorbing segment is specified when
absorption occurs.)
Chapter 5:
- Consider a Cayley tree with coordination number
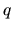 that consists of
that consists of
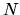 generations. A random walk is initially at the root of the tree.
Determine: (a) the mean first-passage time to get from the root to any site in the
generations. A random walk is initially at the root of the tree.
Determine: (a) the mean first-passage time to get from the root to any site in the 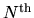 generation, and (b) the mean first-passage
time to get from the root to a specified site in the
generation, and (b) the mean first-passage
time to get from the root to a specified site in the 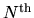 generation, with the condition that the random walk is reflected from all
other sites in the
generation, with the condition that the random walk is reflected from all
other sites in the 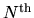 generation.
generation.
- Consider an alternating Cayley tree in which the number of branches at
each new generation alternately bifurcates or trifurcates. Compute the
probability of eventual return to the origin.
- Compute the first-passage probability to reach one corner of an
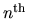 -generation Sierpinski gasket when a random walk begins at another corner
of the gasket.
-generation Sierpinski gasket when a random walk begins at another corner
of the gasket.
Chapter 6:
- Compute the probability for a diffusing particle to eventually hit the
north pole and the south pole of a unit sphere when the particle is initially
on the
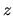 -axis at a distance
-axis at a distance 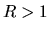 from the center of the sphere. Repeat
the problem for
from the center of the sphere. Repeat
the problem for 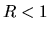 .
.
- Compute the probability that a diffusing particle eventually hits the
northern hemisphere of a unit sphere in
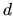 dimensions when the particle is
initially on the
dimensions when the particle is
initially on the 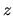 -axis at a distance
-axis at a distance 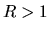 from the center of the sphere.
Repeat the problem for
from the center of the sphere.
Repeat the problem for 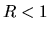 .
.
Chapter 7:
- Consider a diffusing particle that is located at an arbitrary initial
point within a rectangular domain of length
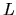 and height
and height 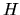 . The particle
is absorbed as soon as it hits the boundary. Compute the probability for the
particle to hit an arbitrary point on the boundary.
. The particle
is absorbed as soon as it hits the boundary. Compute the probability for the
particle to hit an arbitrary point on the boundary.
- Consider a diffusing particle that is located at one focus of an
ellipse of semi-major axis
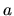 and semi-minor axis
and semi-minor axis 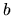 . The particle is
absorbed as soon as it hits the boundary. Compute the probability for the
particle to hit an arbitrary point on the boundary.
. The particle is
absorbed as soon as it hits the boundary. Compute the probability for the
particle to hit an arbitrary point on the boundary.
Chapter 8:
- Consider three identical diffusing particles in one dimension that are
initially located at
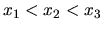 . What is the mean time until
the particle at
. What is the mean time until
the particle at 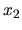 hits its left neighor, its right neighbor,
or either of its neighbors?
hits its left neighor, its right neighbor,
or either of its neighbors?


Next: About this document ...
Sidney Redner
2003-01-25