Statistical Physics
Plamen Ivanov, William Klein, Kirill Korolev, Pankaj Mehta, H. Eugene Stanley
Theorists in statistical mechanics try to understand the behavior of complex systems formed by large numbers of particles in solids, liquids, and complex biological molecules.
Research
- Application of Statistical Physics to Understanding and Preventing Diseases Related to Protein Misfolding, such as Alzheimer Disease

For more than a decade, we have been using our expertise in statistical and condensed matter physics to study the early stages of aggregation of the amyloid beta-protein that eventually makes up the toxic fibrils and plaques found in the brains of Alzheimer patients. We are refining protein-folding models designed to identify the areas of the amyloid protein that are involved in the misfolding process, and to predict forms that the proteins are likely to take in the human brain. The protein structures that the our computer models predict are compared to actual proteins synthesized in the lab by neurological biochemist Dr. David Teplow at UCLA; this dialogue between computational models and observed results ensures that the computer models are accurately mimicking amyloid protein misfolding as it occurs in the brain of an Alzheimer patient.
- Econophysics: Using Statistical Physics Concepts to Better Understand Economic Questions
A physicist views the economy as a collection of interacting units. This collection is complex; everything depends on everything else. The interesting problem is: how does everything depend on everything else? Physicists are looking for laws that will help us understand this complex interaction.
To a physicist, the most interesting thing about economics is that it is dominated by fluctuations in quantities of economic interest. Because big economic shocks affect the economy around the world, the possibility of an economic “meltdown” is one that we must take seriously. Big changes in big money affect not only people with large amounts of it, but also those who have very little of it—those on the margins of society.
Finding ideas that serve to solve economic problems can potentially help in making progress on unsolved physics problems. A good example is turbulence. If we take a bucket of water and disturb the surface, energy is added to the system on a big scale. This energy then dissipates over progressively smaller scales. This is an unsolved physics problem; many empirical facts can be stated, but little can be said about understanding it. The economy is analogous to this example of turbulence. One can add information on a big scale to an economic system—e.g., the news of who wins a presidential election—and that information is dissipated on smaller and smaller scales. The way that you handle the “turbulence” associated with this dissipation of information in a financial market may help us understand how to approach turbulence in our physics research.
- Physical Mechanisms in Liquid Water
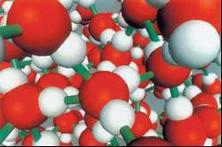
Water is a unique substance. It plays a major role in all living systems, and even small perturbations such as the substitution of deuterium for hydrogen are sufficient to destroy biological function. In living systems, essential water-related phenomena occur in restricted geometries in cells and organelles, and at active sites on membranes. The liquid-liquid phase transition hypothesis arose from molecular dynamics studies on the structure and equation of state of supercooled bulk water and has received some support. Below the hypothesized second critical point, the liquid phase separates into two distinct liquid phases: a low-density liquid (LDL) phase at low pressures and a high-density liquid (HDL) at high pressure. Bulk water near the known critical point at 647 K is a fluctuating mixture of molecules whose local structures resemble the liquid and gas phases. Similarly, bulk water near the hypothesized liquid-liquid critical point is a fluctuating mixture of molecules whose local structures resemble the two phases, LDL and HDL. These enhanced fluctuations influence the properties of liquid bulk water, thereby leading to anomalous behavior. Consistent with this hypothesis are recent MIT experiments, which our group is interpreting. We are also extending our work to the special layer of water surrounding a protein (“hydration water”), which appears to have a dynamic crossover not unlike that observed for water confined in 1D nanopores.
- Research by Sidney Redner
Professor Redner’s research field is non-equilibrium statistical physics. His current interests include the structure of networks, chemical reaction kinetics, and the dynamics of social systems. Professor’s Redner’s recent studies of networks has led to new insights about the link structures of the world wide web and the distribution of citations in scientific publications. He is also applying fundamental approaches from non-equilibrium spin systems to yield insights into opinion formation in populations that are driven by the competing influences of compromise and incompatibility. The ultimate goal is to understand the conditions for consensus or lack thereof in heterogeneous populations that evolve by socially rational rules. Professor Redner also has interests in complex systems, including weather statistics, granular materials, and general stochastic processes.
- Threat Networks and Threatened Networks: Stabilization and Immunization of Networks
Our scientific goal is to uncover common principles governing the behavior of a range of social networks. Our practical goal is to use this understanding to develop specific strategies to destroy threat networks, and in parallel to develop specific strategies to defend threatened social networks against attack. There is evidence that progress toward achieving both goals can be achieved using new approaches from modern statistical physics to social network structure and dynamics that our group has contributed to.
 Physics (Internal)
Physics (Internal)