

Next: Problem 57
Up: Chapter 27
Previous: Problem 13
In preparation for this problem review Conceptual Example
5. A mixture of red light (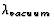 = 661 nm) and
blue light (
= 661 nm) and
blue light (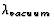 = 473 nm) shines perpendicularly
on a thin layer of gasoline (ngas = 1.40) lying on water
(nwater = 1.33). The gasoline layer has a uniform thickness
of
= 473 nm) shines perpendicularly
on a thin layer of gasoline (ngas = 1.40) lying on water
(nwater = 1.33). The gasoline layer has a uniform thickness
of 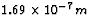 . Destructive interference removes one
of the colors from the reflected light. By means of suitable
calculations decide whether the gasoline looks red or blue in
reflected light.
. Destructive interference removes one
of the colors from the reflected light. By means of suitable
calculations decide whether the gasoline looks red or blue in
reflected light.
SOLUTION:
One of the colors vanishes due to destructive interference.
For destructive interference, the wave which reflects from
the air-gas interface (wave 1, say) must be completely out
of phase with the wave which reflects from the gas-water
interface (wave 2). When wave 1 reflects from the air-gas
boundary, its phase is inverted because air has a lower
index of refraction than gasoline. So, in order for wave 2
to be completely out of phase with wave 1, wave 2 must come
out of the gasoline with the same phase it had going in.
In order to have the same phase, the light must have travelled
one wavelength (or some multiple of wavelengths); i.e.,
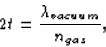
where t is the thickness of the gas layer. So, the wavelength in
vacuum is
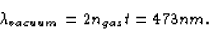
This wavelength just happens to be the wavelength of blue light.
So, since the blue light is destroyed, only the red light remains.
The reflected light looks red.


Next: Problem 57
Up: Chapter 27
Previous: Problem 13
Scott Lanning
4/7/1998
![]()
![]()