

Up: Chapter 27
Previous: Problem 14
The largest refracting telescope in the world is at the
Yerkes Observatory in Williams Bay, Wisconsin. The
objective of the telescope has a diameter of 1.02 m. Two
objects are 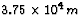 from the telescope. With
light of wavelength 565 nm, how close can the objects be
to each other so that they are just resolved by the telescope?
from the telescope. With
light of wavelength 565 nm, how close can the objects be
to each other so that they are just resolved by the telescope?
SOLUTION:
For minimum angular separation, we use Rayleigh's criterion
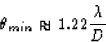
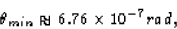
where 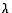 is the wavelength of light and D is the aperature
diameter (of the telescope). If y is the separation and L the
distance to the stars, then, because
is the wavelength of light and D is the aperature
diameter (of the telescope). If y is the separation and L the
distance to the stars, then, because 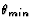 is very small,
is very small,
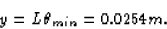
Scott Lanning
4/7/1998
![]()
![]()
![]() is the wavelength of light and D is the aperature
diameter (of the telescope). If y is the separation and L the
distance to the stars, then, because
is the wavelength of light and D is the aperature
diameter (of the telescope). If y is the separation and L the
distance to the stars, then, because ![]() is very small,
is very small,
![]()