

Next: Problem 14
Up: Chapter 27
Previous: Problem 7
A nonreflective coating of magnesium fluoride (n = 1.38) covers
the glass (n = 1.52 of a camera lens. Assuming that the coating
prevents reflection of a yellow-green light (wavelength
in vacuum = 565 nm), determine the minimum nonzero thickness
that the coating can have.
SOLUTION:
We want to choose the film thickness such that destructive
interference occurs between the light reflected from the
air-film interface (call it wave 1) and from the film-lens
interface (call it wave 2). For destructive interference
to occur, the phase difference between the two waves
must be an odd multiple of half-wavelengths.
You can think of the phases of the two waves as second hands
on a clock; as the light travels, the hands tick-tock around the
clock. Consider the clocks on the two waves in question.
As both waves travel to the air-film interface, their clocks both
tick-tock the same time-no phase difference. When wave 1 is
reflected from the air-film boundary, its clock is set forward
30 seconds; i.e., if the hand was pointing toward 12, it's
now pointing toward 6. It's set forward because the index of refraction
of air is smaller than that of the film.
Now wave 1 pauses while wave two goes into and out of
the film. The clock on wave 2 continues to tick as it travels in the
film-tick, tock, tick, tock.... Clock 2 is set forward 30
seconds when it hits the film-lens interface because the index
of refraction of the film is smaller than that of the lens. Then
as it travels back through the film, its clock still continues ticking.
When wave 2 gets back to the air-film interface, the two waves continue
side by side, both their clocks ticking; there is no change in phase
as they continue on their merry way.
So, to recap, since both clocks were shifted forward at the
two different interfaces, there was no net phase shift due to reflection.
There was also no phase shift as the waves travelled into and out from
the air-film interface. The only phase shift occured as clock 2 ticked
inside the film.
Call the thickness of the film t. Then the total distance
travelled by wave 2 inside the film is 2t, if we assume the light
entered pretty much normal to the interface. This total distance
should equal to half the wavelength of the light in the film (for
the minimum condition; it could also be 3/2, 5/2, etc., but that
wouldn't be the minimum thickness) since the hand of the clock
makes one revolution for each distance of one wavelength the
wave travels (right?).
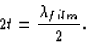
The wavelength in the film is
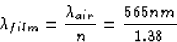
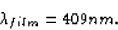
Hence, the thickness should be
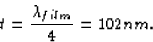


Next: Problem 14
Up: Chapter 27
Previous: Problem 7
Scott Lanning
4/7/1998
![]()
![]()
![]()
![]()