

Next: Problem 49
Up: Chapter 32
Previous: Problem 7
When 1.0 kg of coal is burned, about 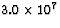 J of
energy is released. If the energy released per 23592U
fission is
J of
energy is released. If the energy released per 23592U
fission is 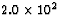 MeV, how many kilograms of coal must
be burned to produce the same energy as 1.0 kg of 23592U?
MeV, how many kilograms of coal must
be burned to produce the same energy as 1.0 kg of 23592U?
SOLUTION: First, we want to determine the energy released by the
uranium in Joules. To do that, note that 1 kg = 1000 g, there are
235 g/mol in uranium, there are 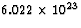 nuclei/mol
by definition of mole, uranium releases 200 MeV per nuclei, and
931.5 MeV =
nuclei/mol
by definition of mole, uranium releases 200 MeV per nuclei, and
931.5 MeV = 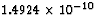 J, (whew!) so that the energy
release by fission in Joules is
J, (whew!) so that the energy
release by fission in Joules is
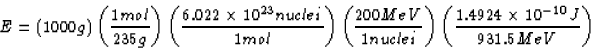
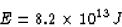
Now, when 1 kg of coal is burned, 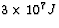 is released.
So the amount of coal need to burn as much energy as 1 kg of
uranium is
is released.
So the amount of coal need to burn as much energy as 1 kg of
uranium is
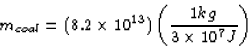
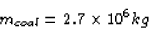
Scott Lanning
4/23/1998
![]()
![]()
![]()
![]()