

Up: Chapter 32
Previous: Problem 25
One proposed fusion reaction combines lithium 63Li (6.015 u)
with deuterium 21H (2.014 u) to give helium 42He (4.003 u):
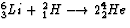 .How many kilograms of lithium would be needed to supply the energy
needs of one household for a year, estimated to be
.How many kilograms of lithium would be needed to supply the energy
needs of one household for a year, estimated to be 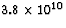 J?
J?
SOLUTION: First, we find the energy released per reaction. Then we'll
find the total amount of lithium needed to produce that much energy.
The missing mass in the reaction is
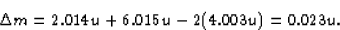
The equivalent of this in energy (converted to Joules) is
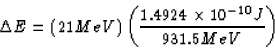
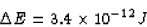
That's the energy per reaction (or energy per lithium nucleus).
The number of nuclei in 1 kg of lithium is
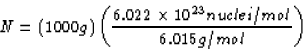
N = 1026 nuclei
Therefore, 1 kg of lithium would produce an energy of
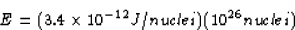
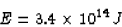
If the energy needed per household per year is 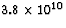 J,
then the amount of lithium required would be
J,
then the amount of lithium required would be
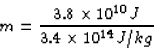
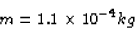
Scott Lanning
4/23/1998
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()