

Next: Problem 52
Up: Chapter 31
Previous: Problem 34
If the activity of a radioactive substance is initially 398
disintegrations/min and two days later it is 285 disintegrations/min,
what is the activity four days later still, or six days after the
start? Give your answer in disintegrations/min.
SOLUTION: The activity of a radioactive substance is defined as
the number of disintegrations per unit time. Since radioactive
decay is random, the number of disintegrations per unit time is
proportional to the number of radioactive atoms; that is,

so the activity is
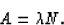
The solution for N(t) is
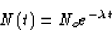
so if we multiply this by 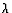 , we get
, we get
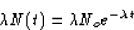
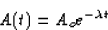
where A(t) is the activity at time t and Ao is the initial activity.
We need to determine 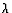
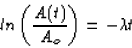
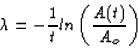
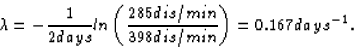
Then we can plug four days into our equation to get the activity
at that time.
A(4 days) = (285 dis/min) e(0.167 days<<55>>-1)(4.00 days)
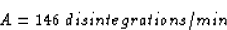
Scott Lanning
4/23/1998
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()