Problem 34

  Iodine ¹³¹₅₃I is used in diagnostic and therapeutic techniques in the treatment of thyroid disorders. This isotope has a half-life of 8.04 days. What percentage of an initial sample of ¹³¹₅₃I remains after 30.0 days?

SOLUTION: Radioactive decay is exponential; that is, if N_o is the original number of particles, and N(t) is the number of particles at time t, then

$$N(t) = N_o e^{-\lambda t}$$

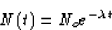
Half-life T_1/2 is defined as the time it takes for there to be remaining half the original number of particles; that is,

$$\frac{N(T_{1/2})}{N_o} = \frac{1}{2} ,$$

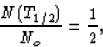
and, combining with the first equation,

$$\frac{1}{2} = e^{-\lambda T_{1/2}}$$

$$ln \left ( \frac{1}{2} \right )= -\lambda T_{1/2}$$

$$ln 2 = \lambda T_{1/2}$$

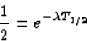
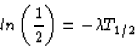
(since ln(a/b) = ln(a) - ln(b), and ln(1) = 0). So, we see that we can relate the decay constant to the half-life

$$\lambda = \frac{ln 2}{T_{1/2}} = \frac{0.693}{T_{1/2}} ,$$

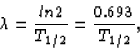
and, in our case,

$$\lambda = \frac{0.693}{8.04 days} .$$

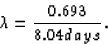
We want the percentage of the original sample remaining after 30 days, or, in other words, we want the ratio N(30 days)/N_o.

$$\frac{N(30 days)}{N_o} = e^{-\left ( \frac{0.693}{8.04 days} \right ) 30 days} = 0.0753 ,$$

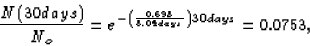
so the percentage remaining is 7.53%.