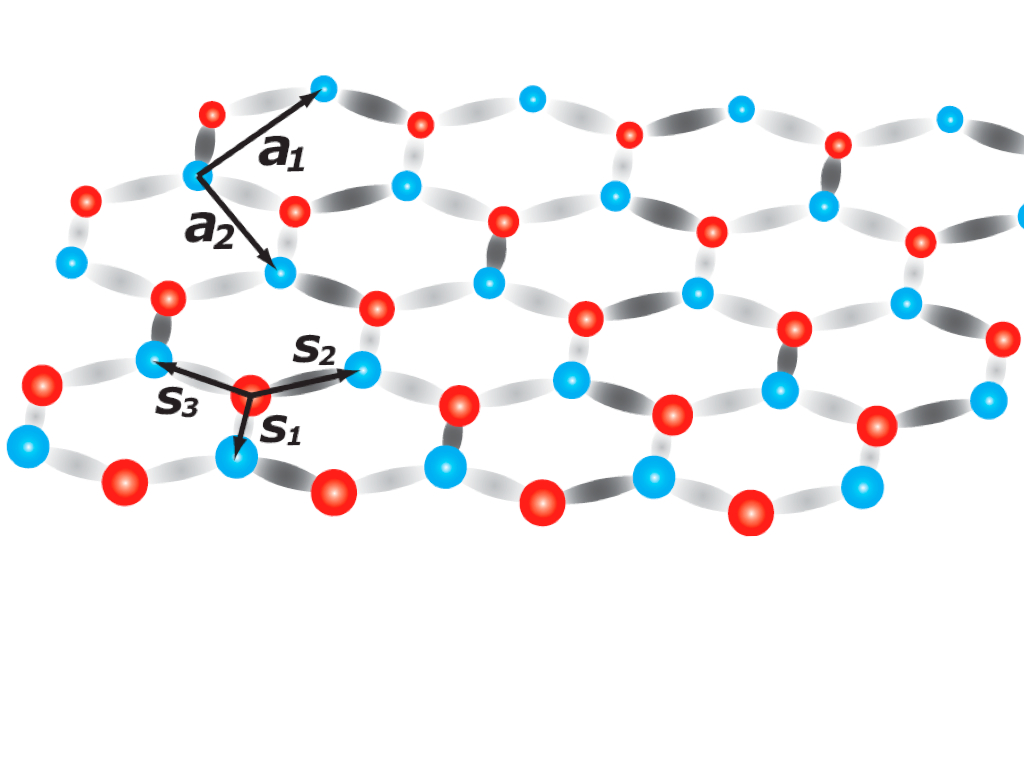
Electron fractionalization is intimately related to topology. In one-dimensional systems, such as polyacetelene, fractionally charged states exist at domain walls between degenerate vacua. In two-dimensional systems, fractionalization exists in quantum Hall fluids, where time-reversal symmetry is broken by a large external magnetic field. Recently, there has been a tremendous effort in the search for examples of fractionalization in two-dimensional systems with time-reversal symmetry.

 

In this research work, we showed that fractionally charged topological excitations exist in tight-biding systems where time-reversal symmetry is respected. These systems are described, in the continuum approximation, by the Dirac equation in two space dimensions. The topological zero-modes are mathematically similar to fractional vortices in p-wave superconductors. They correspond to a twist in the phase in the mass of the Dirac fermions, akin to cosmic strings in particle physics. The quasiparticle excitations can carry irrational charge and irrational exchange statistics. These excitations can be deconfined at zero temperature, but when they are, the charge re-rationalizes to the value 1/2.

 

 

Publications:

C.-Y. Hou, C. Chamon, and C. Mudry,

Phys. Rev. Lett. 98, 186809 (2007)

 

C. Chamon, C.-Y. Hou, R. Jackiw, C. Mudry, S.-Y. Pi, and A. Schnyder,

Phys. Rev. Lett. 100, 110405 (2008)

 

C. Chamon, C.-Y. Hou, R. Jackiw, C. Mudry, S.-Y. Pi, and G. Semenoff,

Phys. Rev. B 77, 235431 (2008)

C.-Y. Hou, C. Chamon, and C. Mudry,

Phys. Rev. B 81 075427 (2010)