
Fractional Chern insulators

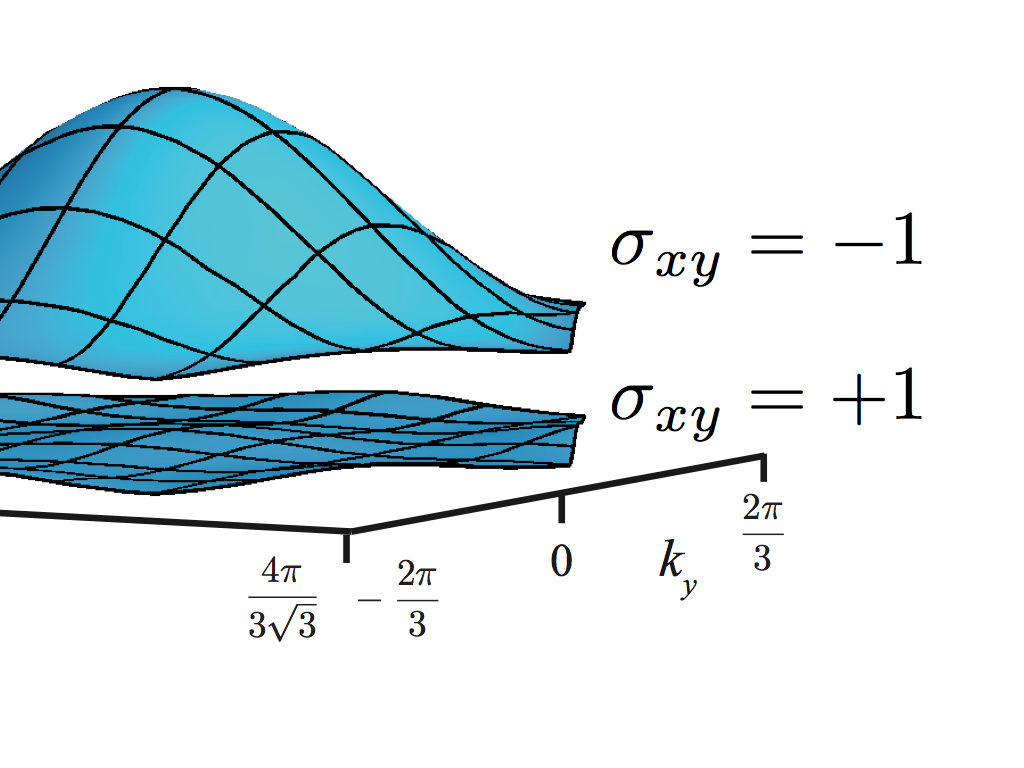
One of the reasons why dispersionless (or flat) bands are interesting is that they accommodate, when partially filled, an exponentially large number of states. This macroscopic degeneracy can be lifted when interactions are added, often leading to rich strongly correlated phenomena. The best known example is the fractional quantum Hall effect (FQHE), which arises from the degeneracy within flat Landau bands for particles in a magnetic field.
In this research work, we have shown that it is possible to isolate flat bands in lattice systems, and that these flat bands can have non-trivial Chern numbers and can sustain, when partially filled, a FQHE. That the ground state of the fractionally filled band is a liquid state is not obvious: a natural competing candidate ground state would be a charge density wave. We have also investigated the strongly interacting version of a Z2 topological insulator, i.e., the case when the bandwidth W for the topologically non-trivial bands is smaller than the interaction energy U (on-site potential), and we have also presented the classification of the Abelian subset of fractional Z2 topological states.
We are currently investigating the possibility of fractional Chern insulators in 3D in systems with chiral symmetry, where dispersionless flat bands naturally arise when the number of bands is odd.
Publications:
Fractional Quantum Hall States at Zero Magnetic Field
T. Neupert, L. Santos, C. Chamon, and C. Mudry,
Phys. Rev. Lett. 106, 236804 (2011)
Fractional topological liquids with time-reversal symmetry and their lattice realization
T. Neupert, L. Santos, S. Ryu, C. Chamon, and C. Mudry,
Phys. Rev. B 84, 165107 (2011)
Time-reversal symmetric hierarchy of fractional incompressible liquids
L. Santos, T. Neupert, S. Ryu, C. Chamon, and C. Mudry,
Phys. Rev. B 84, 165138 (2011)
Topological Hubbard Model and Its High-Temperature Quantum Hall Effect
T. Neupert, L. Santos, S. Ryu, C. Chamon, and C. Mudry,
Phys. Rev. Lett. 108, 046806 (2012)
Noncommutative geometry for three-dimensional topological insulators
T. Neupert, L. Santos, S. Ryu, C. Chamon, and C. Mudry,
Phys. Rev. B 86, 165133 (2012)
Elementary formula for the Hall conductivity of interacting systems
T. Neupert, L. Santos, C. Chamon, and C. Mudry,
Phys. Rev. B 86, 165133 (2012)
Enhancing the stability of a fractional Chern insulator against competing phases
A. G. Grushin, T. Neupert, C. Chamon, and C. Mudry,
Phys. Rev. B 86, 205125 (2012)
Magnetic translation algebra with or without magnetic field in the continuum or on arbitrary Bravais lattices in any dimension
C. Chamon and C. Mudry,
Phys. Rev. B 86, 195125 (2012)