Some examples of how the error scales with the spacing h in numerical integration of a function with an integrable singularity or a peak that is almost singular.

[Problem text here]

We investigate the scaling of the error as a function of the number of intervals N used (h~1/N).

A) Non-singular integrand

These are results along with lines with slope 2 and 3. The expected error scaling for small h is confirmed. Note that there are small deviations from the linear behavior for the largest h, showing the presence of higher-order corrections to the scaling.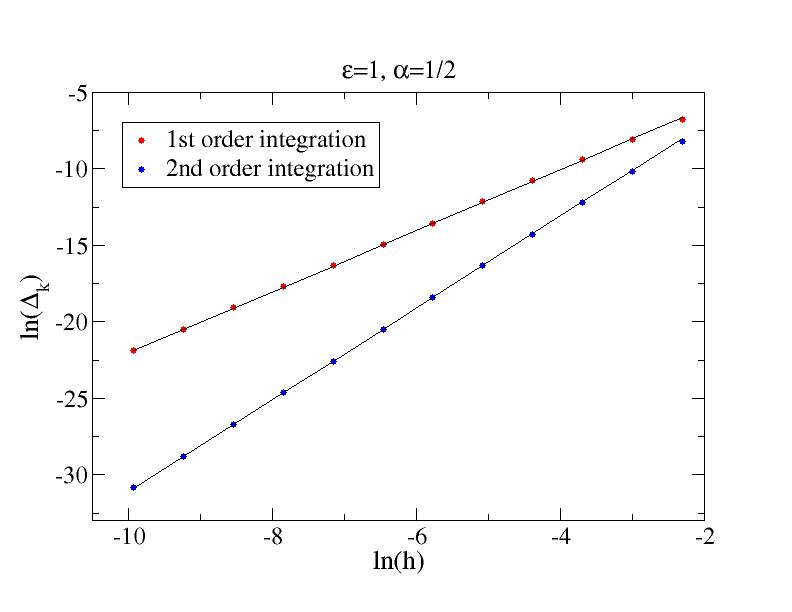

B) Singular integrand

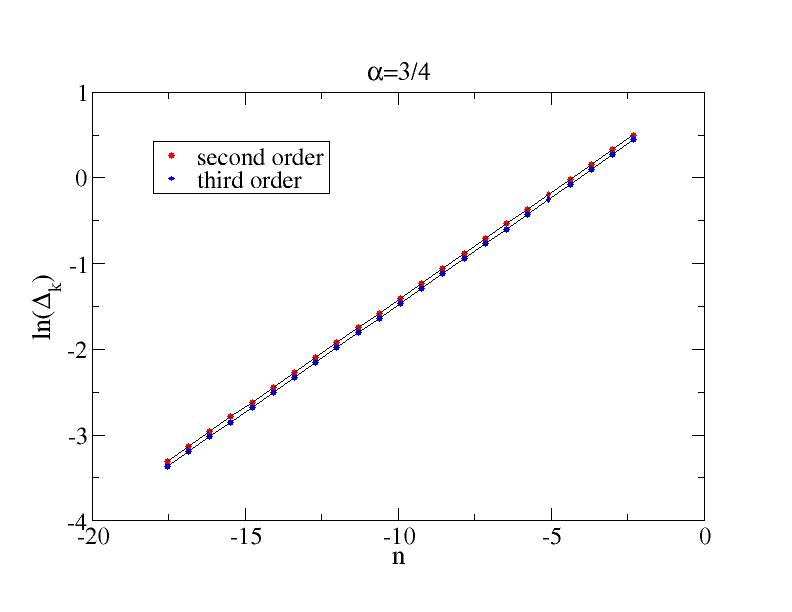
The exponent can be extracted by plottng the logarithm of the error versus log(h) [or log(N) or n].

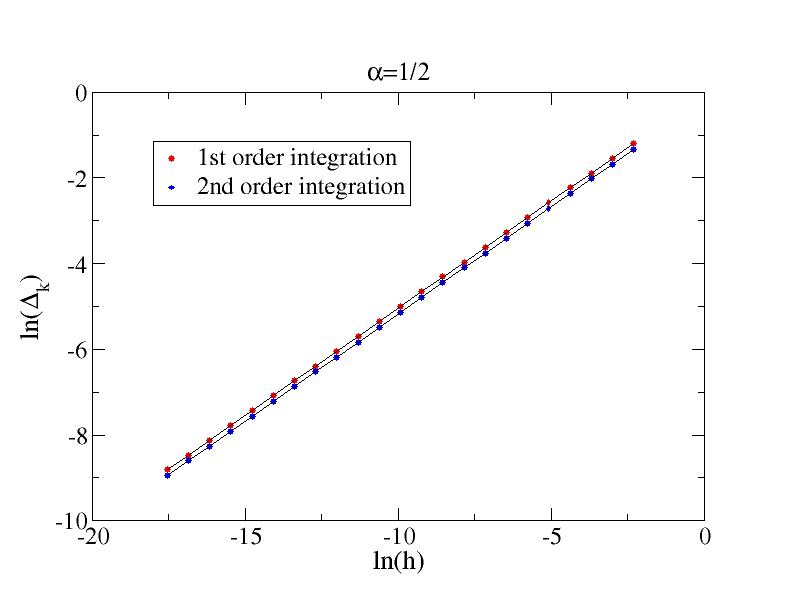
Using a line fitting program (with all errors set to 1 since they are irrelevant but should be the same for every point to give them equal weight in the fit) gave the following exponents (slopes): 
   alpha=1/2, 1st order: slope = 0.49983
              2nd order: slope = 0.50003
   alpha=3/4, 1st order: slope = 0.24996
              2nd order: slope = 0.25001
This is in very good agreement with the expectation; slope=1-alpha.

C) Almost singular integrand

The figure below shows results using alpha=1/2 and epsilon=0.00001.

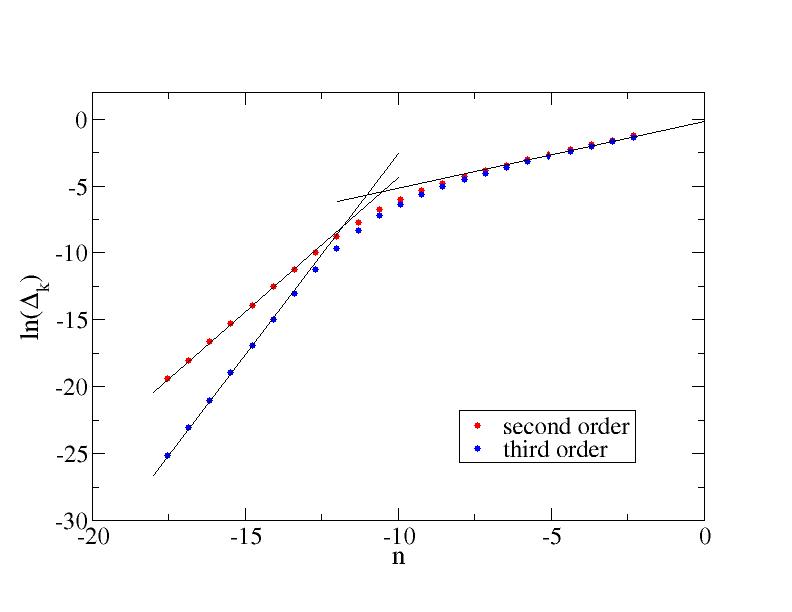
The lines show the expected slopes 1/2 (for h much larger than epsilon) 2 (for h much less than epsilon with 1st-order formula) and 3 (for h much less than epsilon with second-order formula).