

Next: Chapter 24
Up: Chapter 23
Previous: Problem 21
Review Conceptual Example 5. A light bulb has a resistance of 240
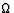 . It is connected to a standard wall socket (120 V,
60.0 Hz). (a) Determine the current in the bulb. (b) Determine
the current in the bulb after a 10.0-
. It is connected to a standard wall socket (120 V,
60.0 Hz). (a) Determine the current in the bulb. (b) Determine
the current in the bulb after a 10.0-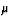 F capacitor is added
in series in the circuit. (c) It is possible to return the current
in the bulb to the value calculated in part (a) by adding an inductor
in series with the bulb and the capacitor. What is the value of the
inductance of the inductor?
F capacitor is added
in series in the circuit. (c) It is possible to return the current
in the bulb to the value calculated in part (a) by adding an inductor
in series with the bulb and the capacitor. What is the value of the
inductance of the inductor?
SOLUTION:
(a) Ohm's Law sayeth

(b) There's no inductor, so XL = 0. The current is given by
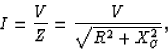
where the impedance of the capacitor is
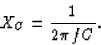
Hence, the current that floweth is
![\begin{displaymath}
I = \frac{120V}{(240 \Omega)^2 + \left [ \frac{1}{2 \pi (60 Hz)
(10 \times 10^{-6} F)} \right ]^2}\end{displaymath}](img11.gif)
I = 0.34 A
(c) In part (a) we only had a resistor, so now we want to add
an inductor in order to cancel the capacitor's impedance. Hence,
in the formula for impedance,
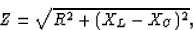
we want to have
XL = XC
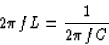
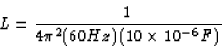
L = 0.704 H .


Next: Chapter 24
Up: Chapter 23
Previous: Problem 21
Scott Lanning
3/23/1998
![]()
![]()
![]()
![\begin{displaymath}
I = \frac{120V}{(240 \Omega)^2 + \left [ \frac{1}{2 \pi (60 Hz)
(10 \times 10^{-6} F)} \right ]^2}\end{displaymath}](img11.gif)
![]()
![]()
![]()