

Next: Problem 32
Up: Chapter 23
Previous: Chapter 23
A circuit consists of a 215-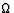 resistor and a 0.200-H
inductor. These two elements are connected in series across
a generator that has a frequency of 106 Hz and a voltage of
234 V. (a) What is the current in the circuit? (b) Determine
the phase angle between the current and the voltage of the
generator.
resistor and a 0.200-H
inductor. These two elements are connected in series across
a generator that has a frequency of 106 Hz and a voltage of
234 V. (a) What is the current in the circuit? (b) Determine
the phase angle between the current and the voltage of the
generator.
SOLUTION:
(a) In order to determine the current in the circuit,
we use the AC version of Ohm's Law
Vrms = Irms Z .
We're given Vrms, so if we find the impedance Z, we can
find Irms. The impedance of the inductor is
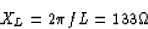
The impedance of the circuit is then
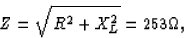
so the current is
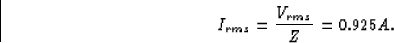
(b) The phase angle between the current and voltage is, by
equation 23.8 (XC = 0),

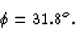
Scott Lanning
3/23/1998
![]()
![]()
![]()
![]()
![]()