Problem 23

  Convex mirrors are being used to monitor the aisles in a store. The mirrors have a radius of curvature of 4.0 m. (a) What is the image distance if a customer is 15 m in front of the mirror? (b) Is the image real or virtual? (c) If a customer is 1.6 m tall, how tall is the image?

SOLUTION:
(a) Radius of curvature of 4 m implies a focal length f = 2 m. So the lens equation gives

$$\frac{1}{d_i} = \frac{1}{f} - \frac{1}{d_o}$$

$$d_i = \frac{1}{\frac{1}{-2 m} - \frac{1}{15 m}} = -1.8 m .$$

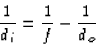
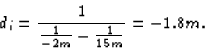
(b) The image distance is negative, so it's virtual .

(c) The height of the object is

$$h_i = -h_o \frac{d_i}{d_o} = -(1.6 m) \frac{-1.8 m}{15 m}$$

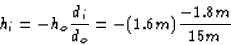
h_i = 0.19 m .