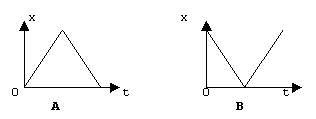
Solutions for PY105

Test 1- Oct 6th 1999

 

 

PROBLEM 1. (10 points)

Answer the following mini-problems with check marks.

(1) Match the following situation (i and ii) to the graphs (A or B) shown below:

  1. (2 points) A ball rolling along the floor away from the origin hits a wall and bounces straight back.

    2. [ X ] A

    [ ] B

  2. (2 points) A ball rolled along the floor toward a wall at the origin hits it and rebounds back.

[ ] A

[ X ] B

 

(2) (3 points) Two balls are launched at the same time from the same height above level ground. Ball A is dropped from rest, while ball B is given a small initial horizontal velocity. Which ball hits the ground first?

[ ] Ball A

[ ] Ball B

[ X] Both balls will reach the ground at the same time

(3) (3 points) A large 500 kg magnet exerts a constant force of 3.00 N on a 0.250 kg bar magnet. What magnitude force does the bar magnet exert on the big magnet?

[ X] 3.00 N

[ ] 1.50 * 10-3 N

[ ] 6.00 * 103 N

 

 

 

 

PROBLEM 2 (20 points)


In towns such as Newton (just west of Boston), there are about 4 medium ponds or lakes used to store water for the approximately 100,000 people who live in the town. Answer the questions below, stating the specific assumptions you have made. (conversion: 2.54 cm=1 inch). Ignore water evaporation or vegetation loss in your calculations.



a.) (10 points) Estimate the total amount of water volume necessary in the four lakes to provide for one year's supply for the town's population.

 

 

Assuming a person consumes about 50liters of water every day,

The total amount of water consumed by population of Newton per year is given by

= (50 liters/person/day)*(365 days/year)*(100,000 people)

= 1.8 * 109 liters/ year

This is the total volume of water necessary in the four lakes in Newton



b.) (10 points) If the local annual rainfall is 30 inches per year, find the area of land necessary to keep the ponds filled and provide the population with water. Express your answer in square kilometers.

If the annual rainfall is 30 inches, then the surface are of the lakes is given by

Area = Volume/depth = (1.8 * 109 liters)/ 30 inches

= 1.8 * 109 liters* (1000 cm3/liter) / (30 inches * 2.54 cm/inch)

= 2.4 * 10 10 cm2 (1km/100000cm)2

= 2 km2

 

 

 

 

 

 

 

Problem 3: (20points)

 

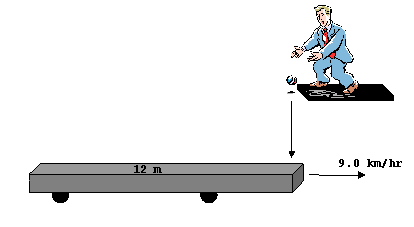
A slowly moving train with 12 m long flatcars is passing a station at 9.0 km/hr. A station manager on an elevated platform drops a rock once every second onto the moving flatcars. Note that the height of the elevated platform is not needed for the answers in parts a and b.

  1. (10 points). If the first rock just hits the front edge of the flatcar, how many rocks will fall onto the car?

In order to compute the total number of rocks in the flatcar, we need to compute the time t taken for the end of a flatcar to pass below the elevated station manager.

Known quantities: v0=9.0km/hr = 9.0km/hr*(1000m/km)/(3600s/hr)=2.5m/s

x0 = 0; x=12m

a = 0 (as the speed of the train is constant at 9.0km/hr

Using x = x0 + v0t + 0.5 a t2 , we get

12m = 0 + 2.5m/s t + 0

t = 12/2.5 s = 4.8 s

In 4.8s, , a total of 5 rocks will fall in the flatcar, Don't forget to add the first one which falls into the flatcar as it passes the station.

 

 

b) (10 points) How many rocks will fall onto the flat car if the train begins to accelerate at 0.50 m/s2 just as the first rock hits the car?

Same as part a, but instead of a=0 we have a=0.50m/s2

Using x = x0 + v0t + 0.5 a t2 , we get

12m = 0 + (2.5m/s) t + 0.5 (0.5m/s2) t2,

or 0.25m/s2 t2 + 2.5m/s t - 12m =0;

need to solve for t from this quadratic equation. We get a negative and a positive solution. We take the positive as negative is unphysical.

Therefore, t = 3.5 s

In 3.5s, a total of 4 rocks will fall in the flatcar.

 

 

 

 

 

 

 

PROBLEM 4. (25 points) Projectile Motion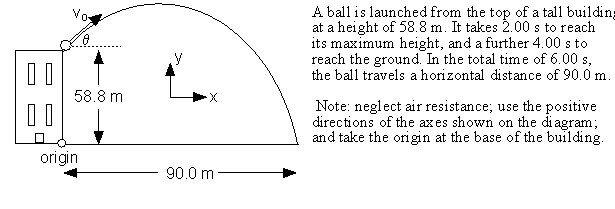

[4 points] (a) What are the x and y components of the initial velocity?

 

In the x direction, the projectile covers 90.0 m in 6.00 s at a constant velocity, because a = 0 horizontally. Therefore, the initial velocity in the x-direction is 90.0/6.00 = 15.0 m/s

In the y-direction, one way to get this is to use v = vo + at. You can use the first two seconds of the motion. After 2.00 s, the projectile is at the maximum height, so its vertical velocity = 0.

a = -9.80 m/s2, so this gives an initial vertical velocity of vo = 9.80(2.00) = 19.6 m/s

You can also use the 6.00 seconds to calculate the initial vertical velocity. Just remember that

y = 0 and yo = 58.8 m. Lots of people had these backwards.

 

[3 points] (b) What is the launch angle, q, as measured from the horizontal?

Tan (q ) = the initial velocity in the y direction / the initial velocity in the x direction

This gives q = tan -1(19.2/15.0), which gives 52.6 degrees.

 

 

[3 points] (c) What are the x and y components of the ball’s velocity just before it strikes the ground?

 

In the x-direction, because there is no acceleration the velocity is constant at vx = 15.0 m/s

In the y-direction, again try v = vo + at. Using vo = 19.2 m/s, a = -9.8 m/s2, and t = 6.00 s, you get a vertical velocity of vy = -39.2 m/s. Note the minus sign!

 

 

 

[3 points] (d) What is the maximum height reached by the ball, measured from the ground?

y = yo + vo t + ½ a t2.

Using yo = 58.8 m, vo in the y-direction is 19.6 m/s, and a = -9.8 m/s2 vertically, this gives:

y = 58.8 + 19.6(2.00) –4.9(2.00) 2 = 58.8 + 39.2 – 19.6 = 78.4 m

[12 points] Using the numbers you calculated above, sketch the x and y components of the position, velocity, and acceleration of the ball during its motion. All graphs are as a function of time. You don’t have to be perfect, but try to do a reasonable job drawing the graphs to scale.

X COMPONENTS Y COMPONENTS

 

 

 

 

 

 

 

 

 

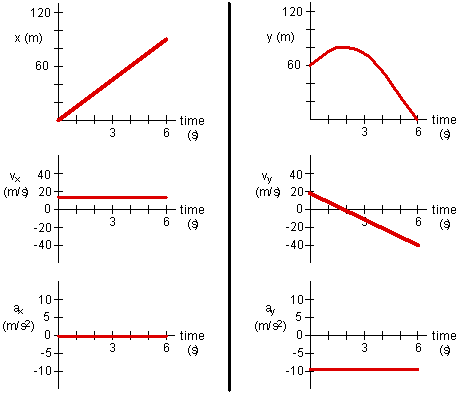
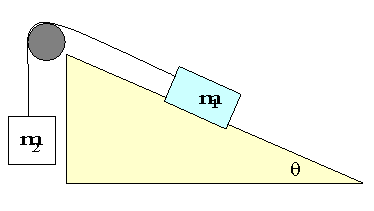
Problem 5. (25 points) Two masses, m2 > m1, are connected by a weightless string and pulley. As shown in the diagram, m1 is placed on an inclined plane which has a rough surface producing a kinetic coefficient of friction m k. The inclined plane makes an angle q with the horizontal. The system is released from rest and observed to move.

 

 

 

 

a. (10 points) Draw a free-body diagram below for each mass showing all the forces acting and their directions.

 

 

 

 

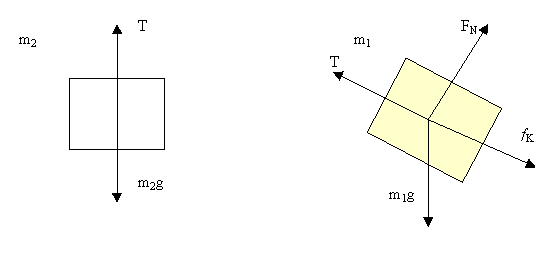
b. (5 points) Using Newton's 2nd Law and the free-body diagrams in part (a), find the acceleration of the masses

Mass 2:

(1) m2g - T = m2a , where down is defined as positive

Mass 1:

(2) T- m1 g sinq - fk = m1a, where up incline is positive

(3) FN= m1g cosq

We also have

(4) fk = m k FN = m k mg cosq

Substituting 4 into 2 we have

(5) T- m1g sinq - m k m1 g cosq = m1a

adding equations 1 and 5 we have

(6) m2g - m1g sinq - m k m1g cosq = (m2 + m2)

solving for a we have

(7) a = g(m2 - m1sinq - m k m1 cosq )/(m1 + m2)

c. (5 points) Assuming that m1 and m2 have masses of 10 kg and 20 kg, respectively, the coefficient of kinetic friction is m k =0 .5 , and the angle q = 60o, find the numerical value for the acceleration of the masses.

 

Mass 2:

a = g(m2 - m1sinq - m k m1 cosq )/(m1 + m2)

Substituting numbers we have

a = 9.8 m/s2 (20 kg - 10 kg x.866- 0.5x10/2 kg)/30 kg)

a= 2.89 m/s2 or 2.9 m/s2 (two significant digits)

 

d. (5 points) For the above case, find the tension, T.

From equation 1

m2g - T = m2a

T = m2g - m2a

T = m2 (g - a)

T= 20 kg (9.8 - 2.9) m/s2

T= 140 Newtons (two significant digits)