We know what the electric field and potential from a point charge look like:

E

=

kQ r2

and

V

=

kQ r

Consider a charged sphere with a symmetrical distribution of charge. Gauss' Law tells us that the electric field outside the sphere is the same as that from a point charge. This implies that outside the sphere the potential also looks like the potential from a point charge.

What about inside the sphere? If the sphere is a conductor we know the field inside the sphere is zero. What about the potential?

Moving from a point on the surface of the sphere to a point inside, the potential changes by an amount:

ΔV = -∫ E • ds

Because E = 0, we can only conclude that ΔV is also zero, so V is constant and equal to the value of the potential at the outer surface of the sphere.

Now consider a solid insulating sphere of radius R with charge uniformly distributed throughout its volume. Once again, outside the sphere both the electric field and the electric potential are identical to the field and potential from a point charge.

What happens inside the sphere? Now the potential is not constant because there is a field inside the sphere. Using Gauss' Law we showed that the field inside a uniformly charged insulator is:

E

=

k Q r R3

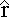Use this to calculate the potential inside the sphere. Starting from some point a distance r from the center and moving out to the edge of the sphere, the potential changes by an amount:

ΔV = V(R) - V(r)

=

–

∫

R     E • ds r

=

–

∫

R     E dr r

=

–kQ R3

∫

R     r dr r

Integrating gives:

V(R) – V(r)

=

– kQ 2R3

(R2 – r2)

V(R) – V(r)

=

– kQ 2R

( 1 –

r2 R2

)

V(R) is simply kQ/R, which can be written as 2kQ/2R, so:

V(r)

=

2kQ 2R

+

kQ 2R

( 1 –

r2 R2

)

Therefore, for r < R,

V(r)

=

kQ 2R

( 3 –

r2 R2

)