| μo I |
| 4π |
dl × 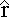
|
| r2 |
We derived an expression for the magnetic field at the center of a circular current loop of radius R. What is the field at some general point a distance x from the center along the axis?
Biot-Savart is appropriate here. Each point on the axis is unique, because the magnetic field changes magnitude as we get further from the center of the loop, so there's no easy way to apply Ampere's Law.
If the current in this loop is out of the page at the top of the loop and into the page at the bottom, in which direction is the net magnetic field on the axis of the loop at some point to the right?
The net field on the axis points along the axis. In our case it points away from the loop, to the right.
When we do the integral all we need to worry about is the components to the right.
| The net magnetic field is | B | = |
|
∫ |
|
Adding up only the x-components, dl × 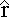 = dl sin(θ)
= dl sin(θ) 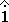
r2 = x2 + R2
| sin(θ) | = |
|
All these are constants, so we get:
| B | = |
|
∫ | dl 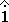 |
∫ dl = 2πR, so
| B | = |
|
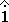 |
When x = 0 we get the correct result for the field at the center of a current loop.
When x is much larger than R the magnetic field falls off as 1/x3.