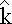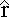What is the magnetic field at some point a distance a from a straight current-carrying wire? We'll split the wire up into pieces of length dx, figure out the field from each piece, and add them up (i.e., integrate) to find the net field.

Define a coordinate system with +x right, +y up, and +z out of the screen. The current is in the +x direction. Put the origin on the wire such that the point where we're calculating field is on the y-axis.

The magnetic field dB from a representative piece of the wire is:

dB = (μ_o / 4π ) I dx × 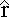/r²

What direction is this field?

The nice thing about this situation is that the field from every part of the wire points in the same direction, out of the page. This means that:

dx × 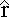= dx sin(θ)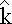

where θ is the angle between the wire and the vector r pointing from ds to the point where we're calculating field.

Our integral for the net field becomes:

B = ( μ_o I / 4π ) ∫ dx sin(θ) /r²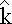

We have too many variables (x, θ, and r) so let's put everything in terms of θ.

a = r sin(θ), so r = a/sin(θ) = a csc(θ)

tan(θ) = -a/x so x = -a/tan(θ) or x = -a cot(θ)

This gives dx = a csc²(θ) dθ

With these substitutions the integral becomes:

B = ( μ_o I / 4π ) ∫ a csc²(θ) sin(θ) dθ /[a² csc² (θ)]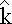

B = ( μ_o I / 4πa ) ∫ sin(θ) dθ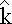

where the limits on the integral run from θ₁ at the left end of the wire to θ₂ at the right end.

Integrating sin(θ) gives -cos(θ), so the result of the integral is:

B = ( μ_o I / 4πa ) [cos(θ₁) - cos(θ₂]