The Biot-Savart Law

Note that you can click-and-drag the purple points around their respective circles to sample the field at different places.

Consider a small piece of wire of length ds carrying a current I. This defines a vector ds that points in the direction of the current. The magnetic field dB set up by this piece of current-carrying wire at a point a distance r away is:

  • proportional to 1/r2

  • proportional to I, the current, and ds, the length of the wire

  • in a direction perpendicular to both ds and r, the vector from the wire to the point

  • proportional to sin(θ), where θ is the angle between ds and r

    All of these observations can be satisfied by the equation:

    dB = (μo / 4π ) I ds × 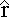/r2

    where the constant μo is known as the permeability of free space and has a value of

    μo = 4π x 10-7 T m /A

    Compare the result for dB to the electric field dE we get from a point charge dq:

    dE = ( 1 / 4π εo ) dq 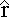/r2

    To find the total field at a point from an entire wire, simply integrate all the dB's:

    Net magnetic field is B = ( μo I / 4π ) ∫ ds × 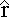/r2

    The process is very similar to what we did to find electric field from charge distributions.