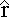
To calculate the field at some point a distance d along the perpendicular bisector of a uniform line of charge of length L, we can simply break the line into tiny pieces, determine the field due to each piece, and then add all these fields as vectors. In other words, we'll integrate.
In general, the integral giving the field from a distribution of charge is:
E = ∫
dE = ∫
k dq / r2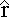
where the unit vector 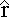points from the charge distribution to the point where the field is being calculated, and reminds us that this is an integral of vectors.
When setting up the integral, take advantage of the symmetry. Consider two pieces of the line, one on the left and one on the right. When these pieces are the same distance from the center of the line the fields they set up are equal in magnitude. The horizontal components cancel, and the vertical components add. The net field has no horizontal component, so in the integral we just need to sum all the vertical components.
The charge Q is spread uniformly over the line, which has length L. There is therefore a constant charge per unit length l which is:
λ = Q/L
If a small piece of the line has a width dx, the charge on it is:
dq = λ dx
The field this piece sets up at the point is:
dE = k dq / r2, where r2 = d2 + x2
Therefore dE = k λ dx / (d2 + x2)
We just need the vertical component, so we multiply by
cos(θ) = d/r = d/(d2 + x2)1/2
dEy = k λ d dx / (d2 + x2)3/2
Summing over the whole line gives:
Ey = ∫ dEy = ∫ k λ d dx / (d2 + x2)3/2
Pulling out the constants:
E = k λ d ∫ dx / (d2 + x2)3/2
the limits on the integral run from x = -L/2 to x = L/2, although you could also do twice the integral from 0 to L/2.
This is a bit of a tricky integral, but looking up the result gives:
∫ dx / (d2 + x2)3/2 = x / [d2 (d2 + x2)1/2 ]
The integral becomes:
Ey = k λ x / [ d (d2 + x2)1/2 ]
Plugging in the limits ( x = -L/2 to L/2) gives:
Ey = k λ L / [ d (d2 + (L/2)2)1/2 ]
λ L = Q, so the field is:
Ey = k Q / [ d (d2 + (L/2)2)1/2 ]
Does the answer make any sense? One check is to plug in the extremes.
If L = 0 (i.e., we're back to a point charge) the field is:
Ey = kQ/d2, which is certainly correct.
If L goes to infinity the result is actually:
Ey = 2 k λ / d.
That's an interesting result, and we'll verify it using another method (Gauss' Law).