[25 points] 5. Refraction.
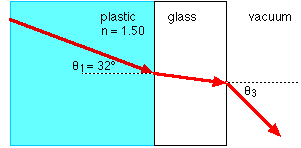
A light ray traveling through some plastic has a frequency of 5.5 x 1014 Hz. It is incident upon a flat slab of glass, making an angle of 32° with the normal to the interface; it passes through the glass and into vacuum, as shown in the sketch. The refractive index of the plastic is 1.50. The refracted ray in the glass has a wavelength of 321 nm.

[5 points] (a) What is the refractive index of the glass?
You might be tempted to write down Snell's law here, but you don't have enough information. What you do know is the wavelength of the light in glass, 321 nm, and you know the frequency. The frequency is the same all the way through - it doesn't change when the light enters another medium.
Multiplying the wavelength by the frequency gives you the speed in the glass:
v = (5.5 x 1014) (321 x 10-9) = 1.766 x 108
m/s.
The index of refraction is n = c / v = 3.00 x 108 / 1.766 x 108 = 1.70.
[10 points] (b) What is the angle of refraction (measured from the normal) for the light ray in vacuum?
Now apply Snell's law. Applying it at the plastic-glass interface gives:
n1 sinQ1 = n2 sinQ2
Note that I'm using Q's here instead of the Greek letter theta!
At the glass-vacuum interface, Snell's law applies again. Because the two sides of the piece of glass are parallel to each other, the angle between the ray and the normal is the same ( Q2 ) at both interfaces. This gives:
n2 sinQ2 = n3 sinQ3
Combining the two equations allows us to ignore the glass (only because the two faces of the glass are parallel) and write:
n1 sinQ1 = n3 sinQ3
The index of refraction in vacuum is 1.00. Plugging in the numbers gives:
1.50 sin32° = 1.00 sinQ3
So the angle is Q3 = 52.6°.
[10 points] (c) What is the minimum angle of incidence (in plastic) for which the ray will be totally internally reflected at the glass-vacuum interface?
We're looking for the critical angle here. A neat way to find it is to just plug n1 and n3 into the critical angle equation and solve. Again, you can do this only because the sides of the glass are parallel to each other. To see why you can do this, remember that at the critical angle, the light ray refracts at 90° to the normal (along the interface, in other words). Applying Snell's law at both interfaces gives:
n1 sinQ1 = n2 sinQ2 = n3 sin90°.
This gives 1.50 sinQ1 = 1.00 sin90°. This gives the critical angle equation:
sinQ1 = 1.00 /1.50
The angle is 41.8°.
[10 points] 6. Refraction and reflection.
Three parallel rays are incident on a converging lens; the lens has a focal
length of 3.0 cm. In each of the two cases below, draw the path of each light
ray and state the x and y coordinates of the point where the rays converge.
Assume the lens lies at the origin of an x-y coordinate system, and the grid
has a spacing of 1 cm by 1 cm.
[5 points] (a) The rays are parallel to the principal axis, and shine on the upper half of the lens.
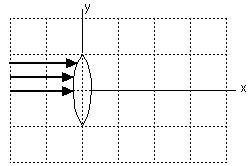
The lens brings all these paraxial rays (rays parallel to the principal axis) to the focal point. The diagram should show each ray going through the focal point, 3 cm to the right of the lens.
The rays converge at: x = 3 cm, y = 0 cm
[5 points] (b) The rays are parallel to the principal axis; a plane mirror is placed at x = 2 cm, parallel to the y-axis.
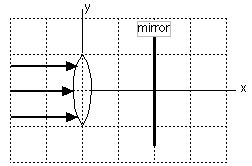
Again, the rays head off towards the focal point. The mirror intercepts them, and they reflect back obeying the law of reflection. Instead of converging 1 cm behind the mirror, they will converge 1 cm in front of the mirror (after reflecting!). In some sense, the focal point is reflected in the mirror.
The rays converge at: x = 1 cm , y = 0 cm