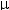 C charge located 3 cm to the left of a given point. Where can we place a -1
C charge located 3 cm to the left of a given point. Where can we place a -1 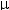 C charge so that the electric potential at the point is zero?
C charge so that the electric potential at the point is zero?
Consider a +3 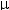 C charge located 3 cm to the left of a given point. Where can we place a -1
C charge located 3 cm to the left of a given point. Where can we place a -1 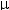 C charge so that the electric potential at the point is zero?
C charge so that the electric potential at the point is zero?
First, let's ask where along the line joining the +3 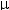 C charge and the point we could place the -1
C charge and the point we could place the -1 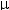 C charge to make the potential zero. In how many places can you put the -1
C charge to make the potential zero. In how many places can you put the -1 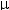 C charge to make V = 0 at the point?
C charge to make V = 0 at the point?
How can we find these points exactly? We know:
We need to solve:
k (+3 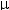 C) / 3 cm + k (-1
C) / 3 cm + k (-1 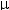 C) / r = 0
C) / r = 0
When we cancel out the factors of k and 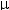 C, we get:
C, we get:
+ 3 / 3 cm - 1 / r = 0 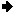 r = 1 cm
r = 1 cm
If you place the -1 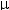 C charge 1 cm away from the point then the potential will be zero there. There are two places along the line that will work: 1 cm to the left of the point and 1 cm to the right of the point. (You should verify this using the simulation.)
C charge 1 cm away from the point then the potential will be zero there. There are two places along the line that will work: 1 cm to the left of the point and 1 cm to the right of the point. (You should verify this using the simulation.)
Are there other places that you could put the -1 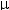 C charge to make the potential zero at the point, perhaps not along the line?
C charge to make the potential zero at the point, perhaps not along the line?
The answer we obtained (r = 1 cm) says that all you need to do is place the -1 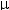 C charge 1 cm away from the point. There was no reason that it had to be 1 cm to the left or the right of the point. It can in fact be 1 cm in any direction. So there are an infinite number of places that you can put the -1
C charge 1 cm away from the point. There was no reason that it had to be 1 cm to the left or the right of the point. It can in fact be 1 cm in any direction. So there are an infinite number of places that you can put the -1 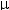 C charge to make the potential zero: these places form a circle of radius 1 cm centered about the point.
C charge to make the potential zero: these places form a circle of radius 1 cm centered about the point.
The freedom of not worrying about direction is because potential is a scalar, that is, just a number. The +3 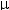 C charge creates a potential (just a number) at the point. The -1
C charge creates a potential (just a number) at the point. The -1  C charge must be placed so that its potential at the point is the negative of that same number. On the other hand, a field has both a magnitude and a direction. If we wanted to ask the same problem as before except that you had to place the -1
C charge must be placed so that its potential at the point is the negative of that same number. On the other hand, a field has both a magnitude and a direction. If we wanted to ask the same problem as before except that you had to place the -1  C charge to make the electric field zero at the point, then there would only be one place to put it: along the line to the left of the point. (See the electric field Physlab: "Example - is the Field Zero?") This is the only place where the vectors had both the same magnitude and opposite directions.
C charge to make the electric field zero at the point, then there would only be one place to put it: along the line to the left of the point. (See the electric field Physlab: "Example - is the Field Zero?") This is the only place where the vectors had both the same magnitude and opposite directions.