Potential Energy of a Charge in an Electric Field

Just as a mass in a gravitational field has a gravitational potential energy, a charged particle in an electric field has an electric potential energy. A mass in a uniform gravitational field has a potential energy, U, given by:

U = mgh where

• m is the mass of the particle
• g is the value of the uniform gravitational field
• h is the perpendicular distance from an arbitrarily chosen level where we define U=0 (usually the ground)

Recall that the work done by the gravitational force, F = mg, is the negative of the change in gravitational potential energy. So when the mass falls from a height h_A to a height h_B the work done by the force is:

W_AB = mgh_A - mgh_B

Similarly, the potential energy of a charged particle in a uniform electric field is:

U = qEd where

• q is the charge of the particle
• E is the value of the uniform electric field
• d is the perpendicular distance from an arbitrarily chosen line where we define U=0

So the work done by the electric force, F = qE, when the charge moves from a distance d_A to a distance d_B is:

W_AB = qEd_A - qEd_B

Note that the positive charge acts like the mass in that it accelerates in the same direction as the field. The negative charge, however, accelerates in the opposite direction as the field as we saw in a previous Physlab.

Two charges - Click on the milestone icon to answer a conceptual question that will appear in the milestone window at the upper right. Click the Explanation button to see a detailed solution to the milestone question.

In Milestone 1, if both particles are released from rest from a height of 10 cm, what is the difference in their velocities when they each pass through U = 0? Assume that Q = 2 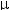C and the mass of each particle is 1 g. Do not neglect gravity. (Hint: you will need to measure the strength of the electric field and use conservation of energy principles.)

Two particles interacting have a potential energy because of their interaction. Recall that in gravity, the potential energy of two masses, m and M, separated by a distance r, have a potential energy given by:

U = GMm/r

Similarly, two charges, q and Q, separated by a distance r, point charge, Q, have a potential energy given by:

U = kQq/r

In the above simulation, verify the 1/r dependence for yourself using the information next to the movable charge. Notice that if you press the play button, the charge will accelerate. Where can you place the charge so that the acceleration is greatest?

As for the uniform field, the work done by the non-uniform field is the negative of the change in potential energy.

Two masses - Click on the milestone icon to answer a conceptual question that will appear in the milestone window at the upper right. Click the Explanation button to see a detailed solution to the milestone question.

Answer to question:

• v_2Q - v_Q = 0.12 m/s