If the mass of the charge in the above simulation is 0.5 mg and the electric field is 1000 N/C, then what is the magnitude of the charge? (Hints: F = ma = qE. Use the data table and projectile equations to determine the acceleration.)
The form of the electrostatic force should remind you of something that you have already seen before: gravity. Recall that the gravitational force is:
F = Gm1m2/r2 where G = 6.67 x 10-11 Nm2/kg2
Compare this to the electrostatic force studied in the previous Physlab:
F = kq1q2/r2 where k = 8.99 x 109 Nm2/C2
Comparing these two forces, it is clear that the charge in electrostatics plays a similar role to that of the mass in gravity. A major difference is that while the gravitational force is always attractive, the electrostatic force can be either attractive or repulsive.A situation involving gravity that we encountered frequently was that of a projectile, where one mass m1, the projectile, interacted with a much larger mass m2, the Earth. In this case we wrote the force on the projectile as:
F = m1g where g = Gm2/r2 (m2 is the mass of the Earth and r is the radius of the Earth)
We commonly referred to g as "the acceleration due to gravity". It is more accurate to call g the gravitational field produced by the Earth at the surface of the Earth. A field has a magnitude and direction at every point in space. The field line pattern in the simulation represents the uniform gravitational field near the surface of the Earth. The direction is down as indicated by the arrows and the equal spacing of the field lines indicates that the magnitude is the same everywhere.
Now consider a positive charge that is launched horizontally into a uniform electric field. The charge will act the same way in an electric field as the mass did in a gravitational field. We can write the force on the charge as:
F = qE where E is the electric field.
If the mass of the charge in the above simulation is 0.5 mg and the electric field is 1000 N/C, then what is the magnitude of the charge? (Hints: F = ma = qE. Use the data table and projectile equations to determine the acceleration.)
Notice that the above equation is a vector equation. If the charge is positive, then the force will be in the same direction as the electric field and if the charge is negative, the force will be in the opposite direction as the electric field. For instance, look at what happens when we launch a negative charge horizontally into a uniform downward electric field.
| A charge on a string -
Click on the milestone icon to answer a conceptual question that will
appear in the milestone window at the upper right.
|
The gravitational field near the surface of the earth is uniform. But what happens to the gravitational field produced by the Earth at a point that is halfway to the Moon? Recall that g = Gm2/r2 where m2 is the mass that is producing the gravitational field (in this case the Earth) and r is the distance from the center of mass of m2 to the point where we want to know the field. Therefore, the further you get from the Earth the smaller the magnitude of the Earth's gravitational field.
Consider the Moon orbiting the Earth. The gravitational field vectors produced by the Earth are shown in the simulation. The Moon feels a force directed along the field vectors, that is, always toward the Earth. This is the force that keeps the Moon in its orbit around the Earth.
Now consider the Hydrogen atom: an electron (negative charge) orbiting a proton (positive charge). Because of the electric field produced by the proton, the electron feels a force directed toward the proton. This is the force that keeps the electron in its orbit around the proton.
| A hydrogen atom -
Click on the milestone icon to answer a conceptual question that will
appear in the milestone window at the upper right.
|
Answer to question:
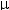C