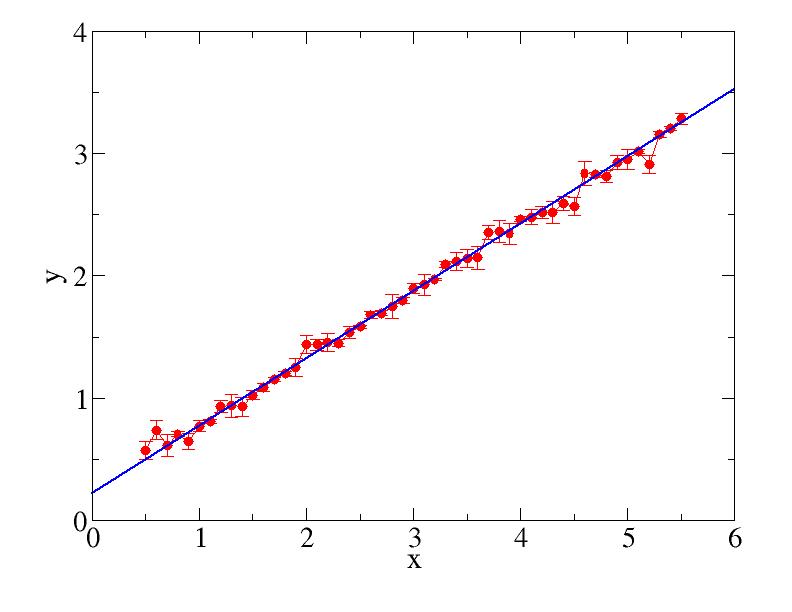
We often encounter the problem of finding the line that best reproduces (fits) the behavior of numerical data (from calculations or experiments). Often the data have error bars, i.e., we have points x(i),y(i),s(i), where i=1,....,N and s(i) is the standard deviation of y(i).

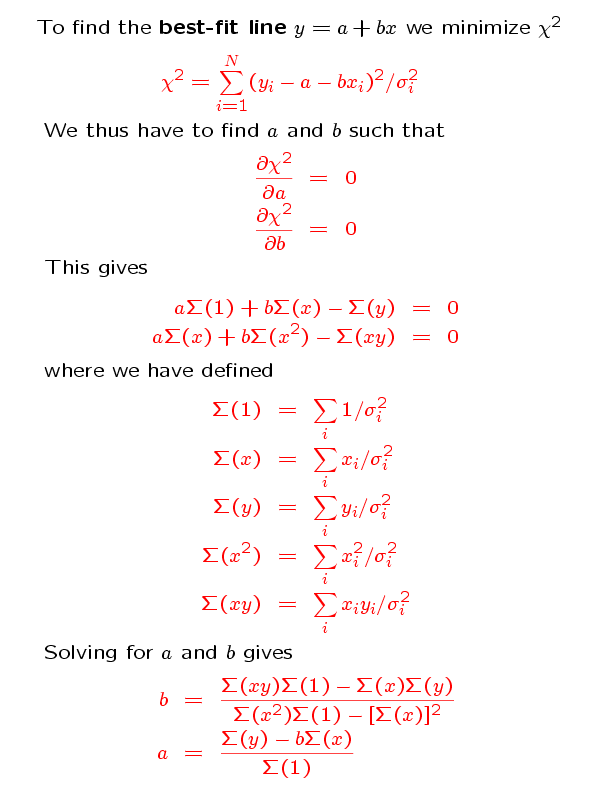
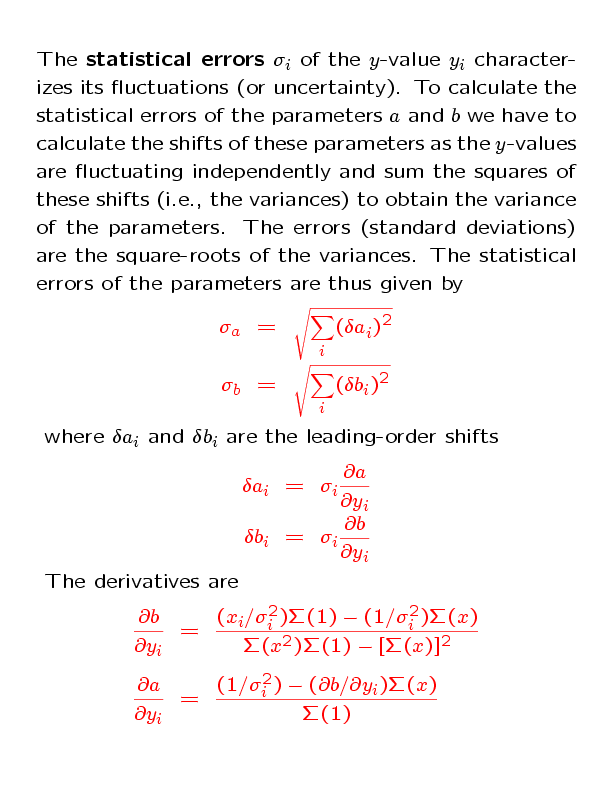
This is a Fortran 90 line-fitting program [linefit.f90]

 Intercept and expected error :  0.22112252494404125 0.009332726022970368
 Slope and expected error     :  0.5506251596885045 0.002800789912660865
 Number of data points        :  51
 X2 per degree of freedom     :  1.170613622829978

The data was generated by adding noise (distributed according to Gaussians with mean 0 and variable width equal to the stated errors) to a line y=a+bx with a=0.23 and b=0.55. These parameters are seen to be reproduced by the fitting program to within statistical errors.