[simulation code (Fortran)] [averaging code]

Part 1 (pure ferromagnetic model)

The purpose of this part of the assignment is to investigate the behavior of the solution as a function of the time step in the RK integration.

The figures below shows the "success probability", i.e., the probability of the system being in the classical (s=1) ferromagnetic ground state, as a function of s for a system with N spins. At s=0 the probability is trivially given by 1/2^(N-1) for a system of N spins, since the starting state is the equal superposition of all spin states (and note that there are two ferromagnetic states).

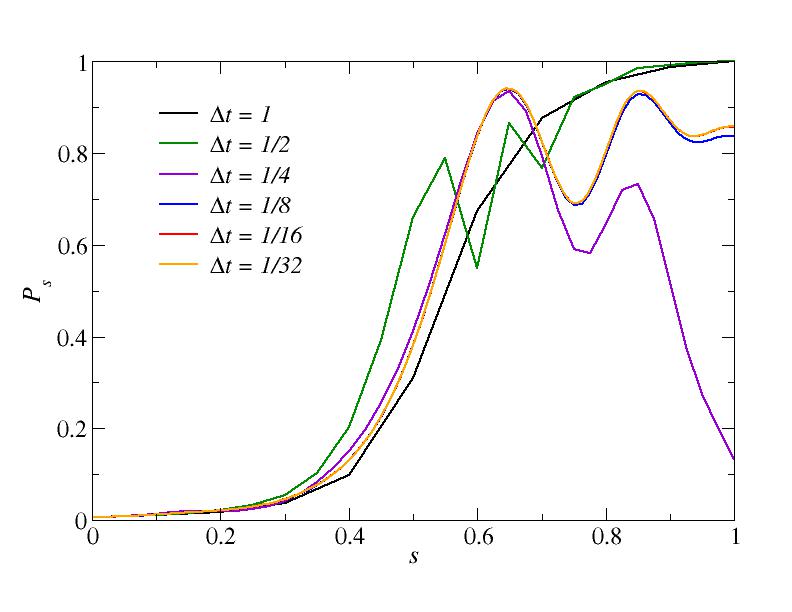This figure is for total time T=10, i.e., velocity v=0.1.

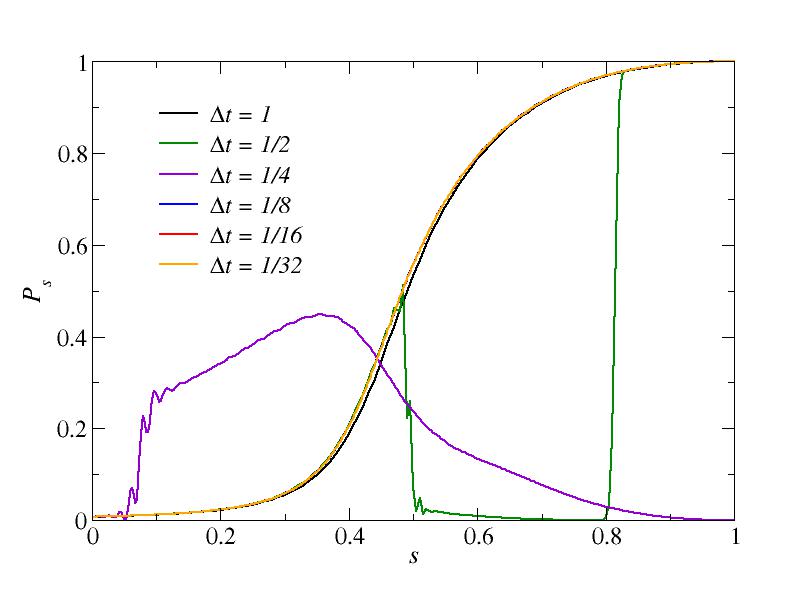This figure is for total time T=100, i.e., velocity v=0.01.

Note that the behavior when the time step is very large (0.5 and 1) is non-monotonic and not represesentative of the way the curves converge to the correct solution for smaller time steps. For T=100 the solution is apparently completely unstable for some values of the time steps. Note that the curves for the smallest times steps fall essentially on top of each other and are hard to distinguish.

The excess energies (Ising energy above the ground state energy at s=1) are shown in the curves

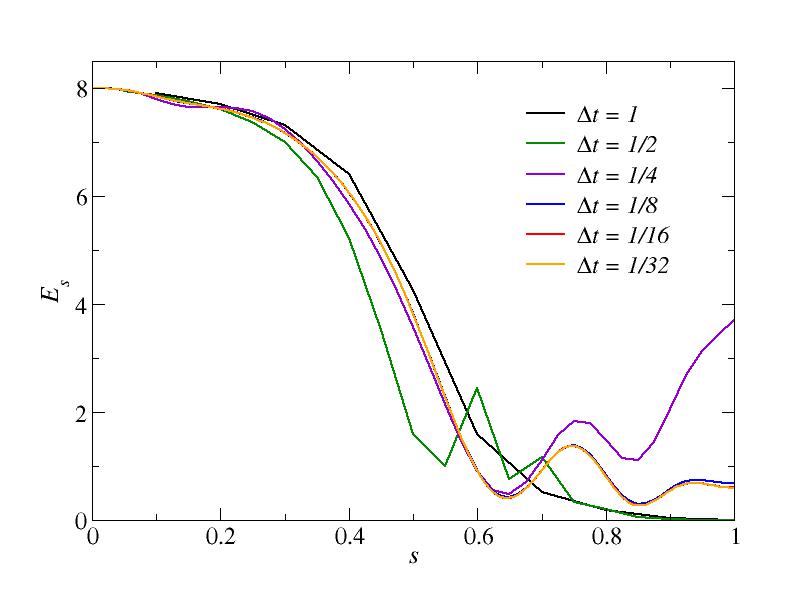This figure is for total time T=10, i.e., velocity v=0.1.

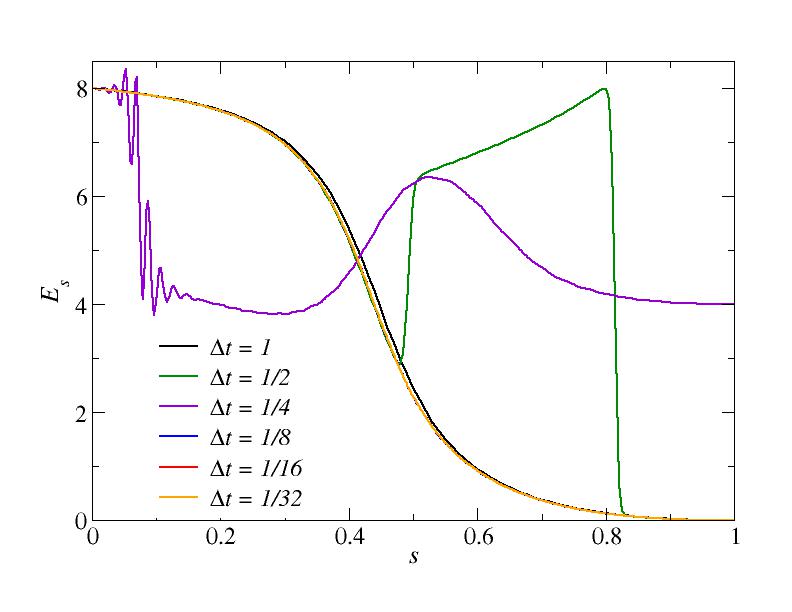This figure is for total time T=100, i.e., velocity v=0.01.

Part 2 (mixed ferromagnetic and antiferromagnetic couplings)

Here the purpose is to study systems with frustrated interactions, i.e., mixed ferromagnetic and antiferromagnetic nearest-neighbor couplings. The parameter "a" is the probability of a coupling to be negative and is a measure of the degree of frustration. We expect it to become harder to find the ground state as a is increased.

First, let us look at an example of the time evolution from s=0 to s=1. The graphs below show results for system size N=8, annealing velocity v=1/128, and three different values of the negative-coupling probability

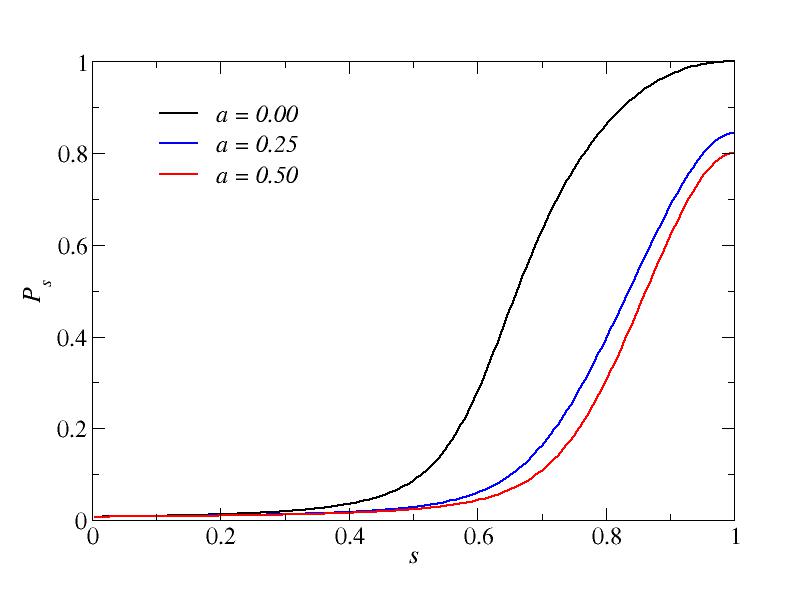Success probability; N=8, v=1/128.

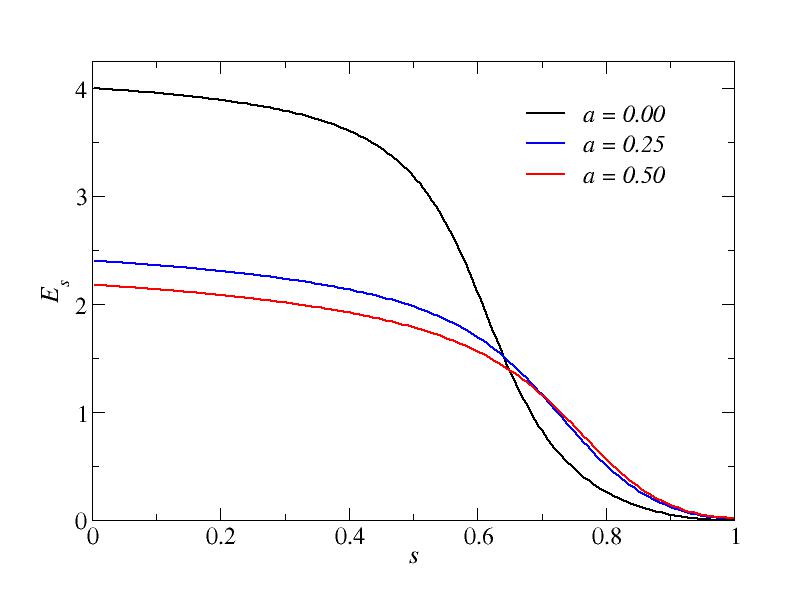Excess energy; N=8, v=1/128.

The results confirm the notion that the presence of frustrated couplings makes it harder to reach the ground state (i.e., Ps becomes smaller and Es becomes larger at the classical, s=1, point).

Next, let us look at the success rate at the final point (s=1) as a function of the annealing velocity and the system size. The three figures below show results for the success rate for three different values of a, graphed on the same scales in order to facilitate comparisons.

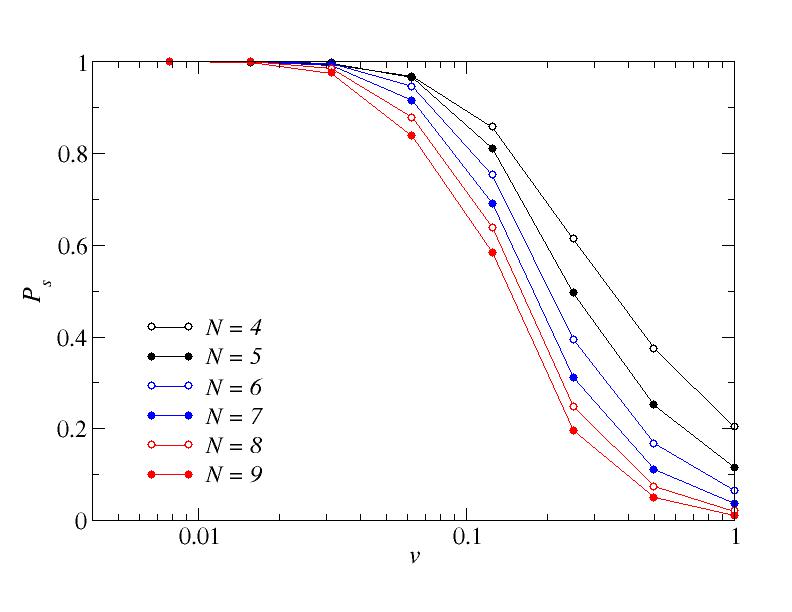a=0. Success probability when the final classical (s=1) point has been reached.

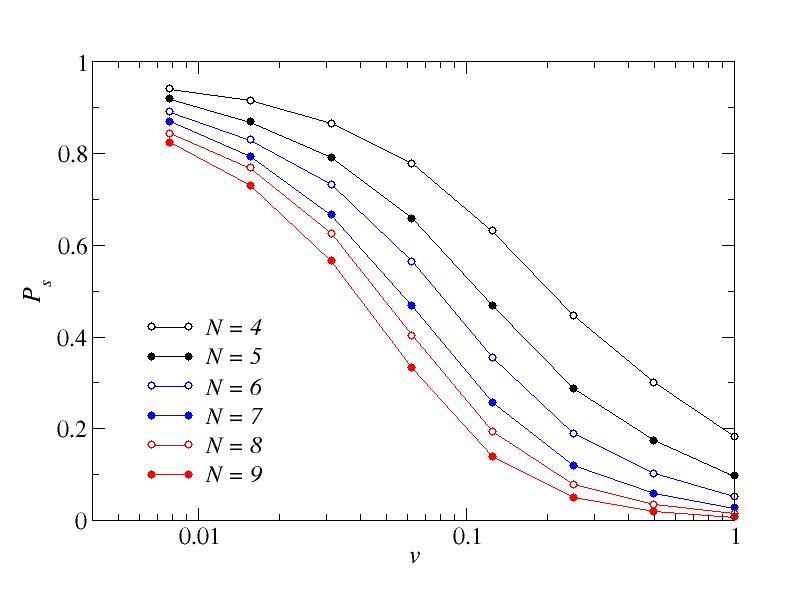a=1/4. Success probability when the final classical (s=1) point has been reached.

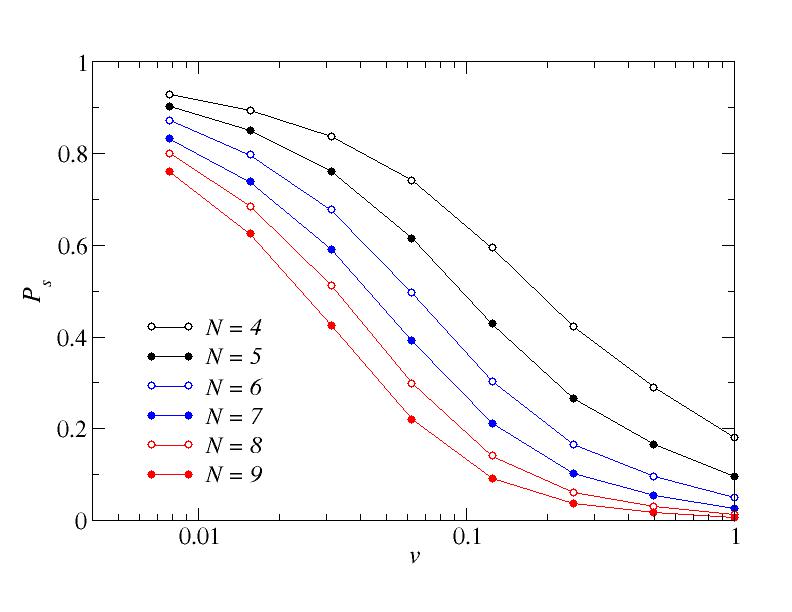a=1/2. Success probability when the final classical (s=1) point has been reached.

The following three graphs show the corresponding excess Ising energies.

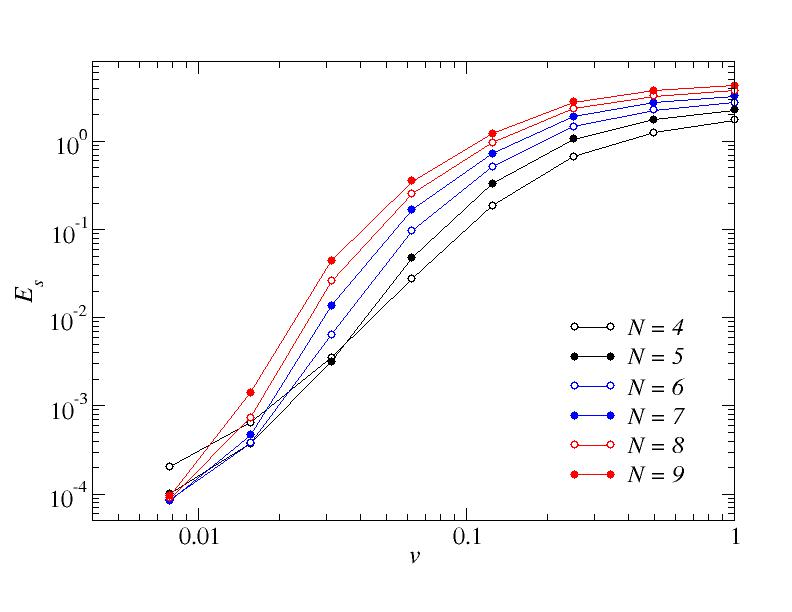a=0. Excess Ising energy when the final classical (s=1) point has been reached.

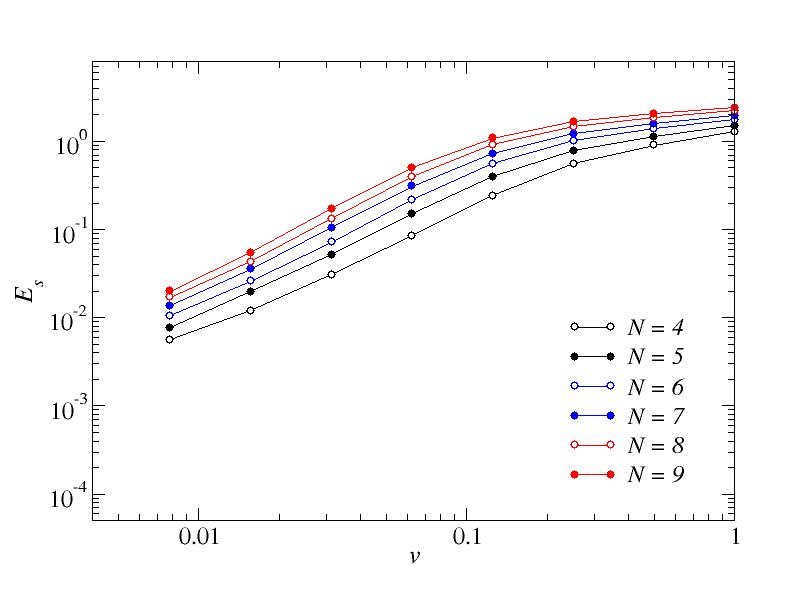a=1/4. Excess Ising energy when the final classical (s=1) point has been reached.

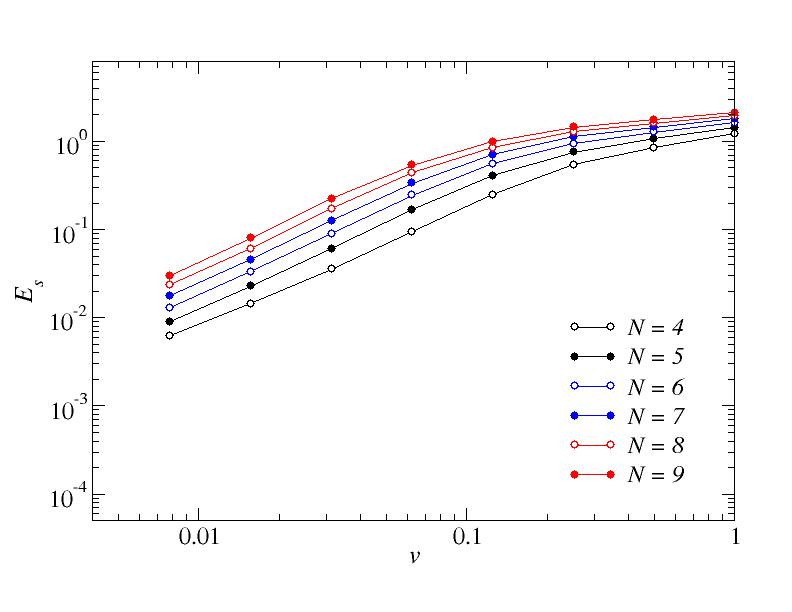a=1/2. Excess Ising energy when the final classical (s=1) point has been reached.

These results carry the same message as the success probability.

Finally, let us look at the system size dependence when the velocity has the lowest value considered here; v=1/128.

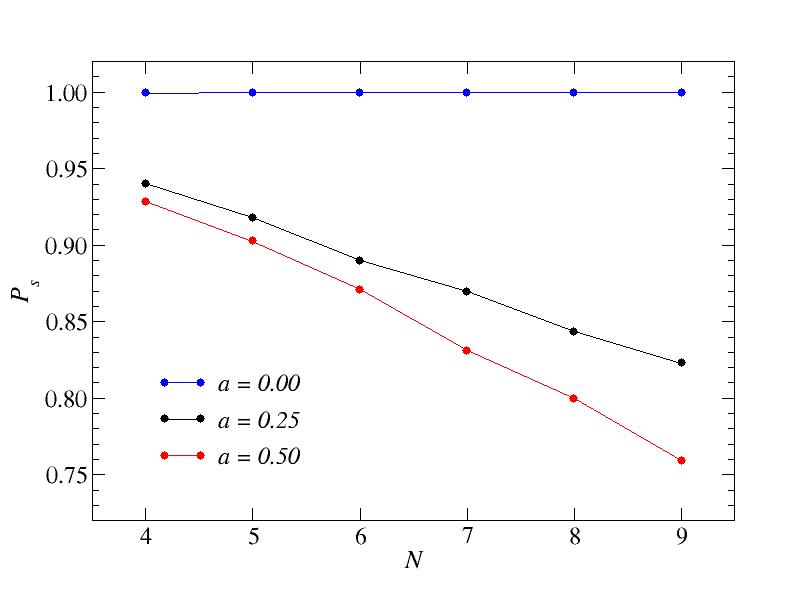Success probability versus system size for v=1/128.

Here it looks very clear that there is a really drastic change in going from a=0 (no frustration) to a>0. The success rate is very close to 1 for a=0 but drops well below 1 for a=1/4 and there is a further drop when increasing to a=1/5.

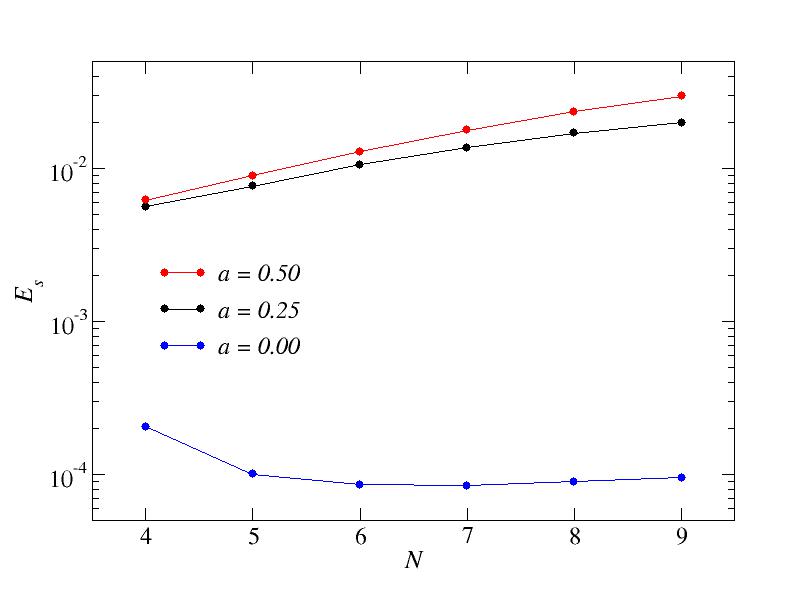Excess Ising energy versus system size for v=1/128.

The excess energy is very small for a=0. Note that initially the excess energy drops with increasing N. It is not completely clear why, but likely it is because the density of low-energy states increases. For larger N the energy also increases, as for the a>0 cases.

In practice, the excess energy may be a better measure of success because one is not nessessarily interested in just the fully optimized solution, but in a solution which has some cost function (corresponding to Es) not exceeding some certain threshold value. Note that the density of states for this random Ising model (with normal distributed couplings) increases rapidly as the system size increases, so the number of acceptable solutions also increases with N. Nevertheless, it also becomes harder with increasing N to find acceptable solutions.

The systems studied here are very small. In a real quantum annealer for optimization, one would use hundreds or thousands of qubits for challenging optimization problems. Clearly the present results can not be easily extrapolated to such large N, but it is nevertheless obvious that quantum annealing for these fully-connected frustrated systems is not an easy task.

Note that we have used units in which hbar=1 and the couplings are normalized in a certain way (as described in the assignment). To convert to real time units, one just has to normalize v with the correct value of hbar and the energy scale of the couplings corresponding to the device used.