Solutions for homework assignment #3

Solution program (Fortran) [geostat.f90]
Solution program (Gabe's Jupyter notebook) [hw3_sol.ipynb]

Problem A (the moon moving in the equatorial plane)

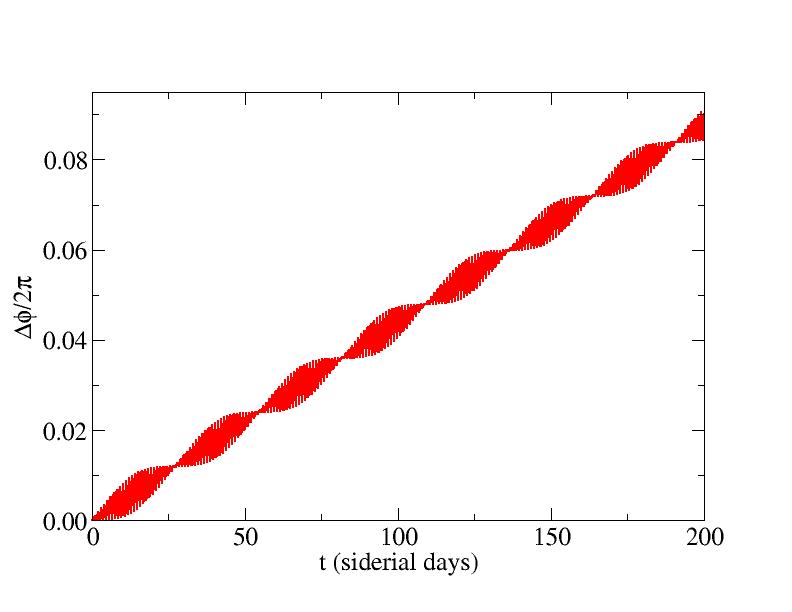
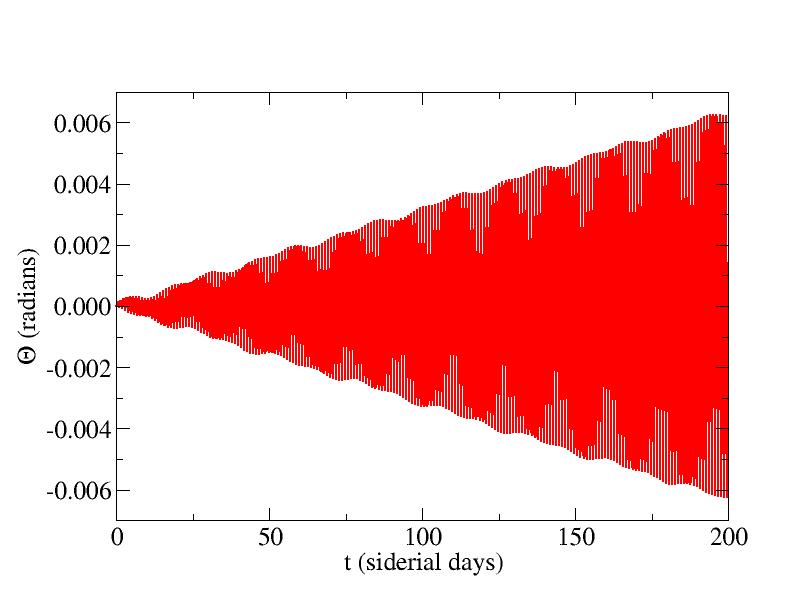
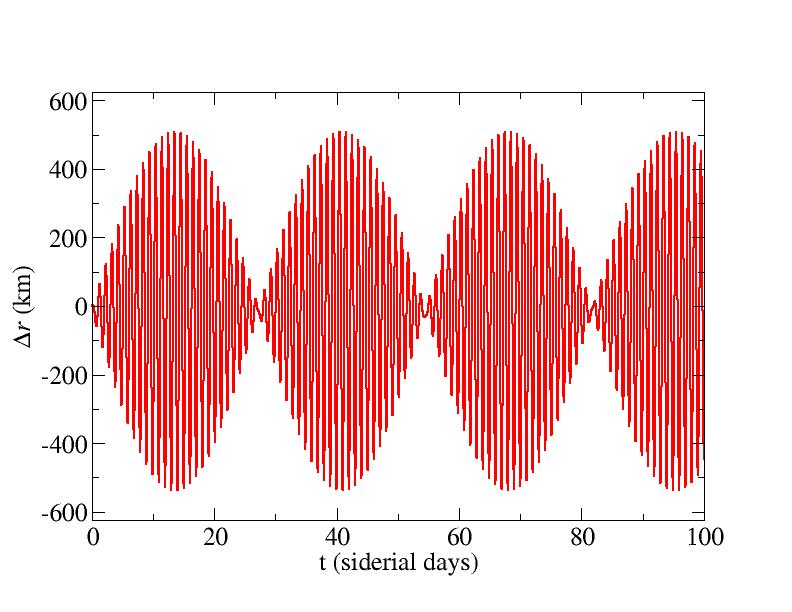
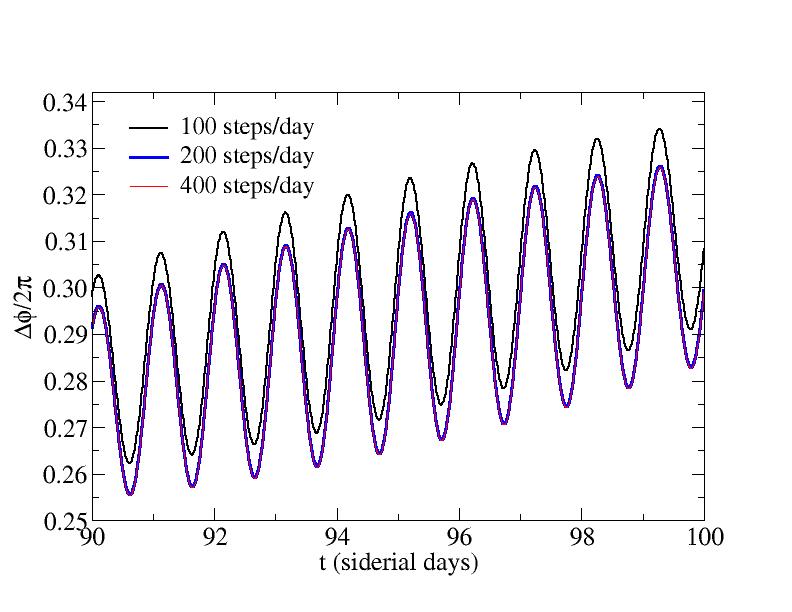
The deviation of the angular position of the satellite from its position in the absense of the moon is shown in the figure. After 100 days, the deviation is approximately 18 degrees, and hence the satellite's position must clearly be adjusted regularly to keep it above the desired location. This calculation used 500 integration steps per day.
The next figure shows the relative deviation of the altitude from the geo-stationary altitude. The maximum deviation is about 500 km, or more than 1%. Note that the fluctuations exhibit almost, but not quite, periodicity corresponding to the moon's period of 27.25 days.
The figure below shows the angular deviation in the time range 90 to 100 days calculated using different numbers of integration steps per day. The result for 200 and 400 steps per day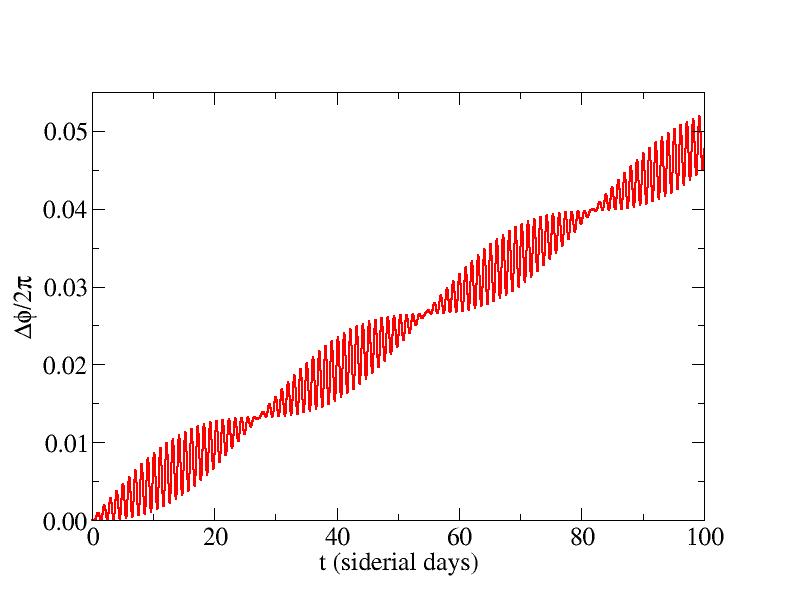 can barely be distinguished.

Compensating for the drift

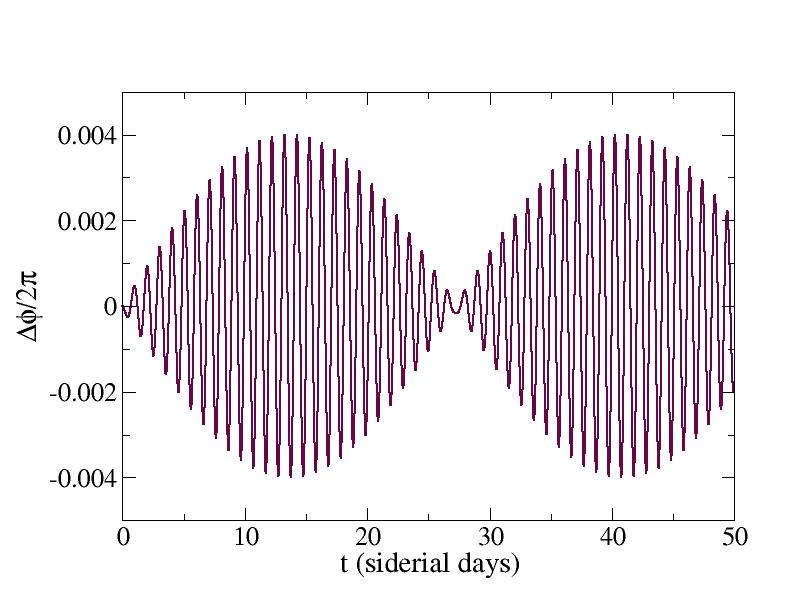
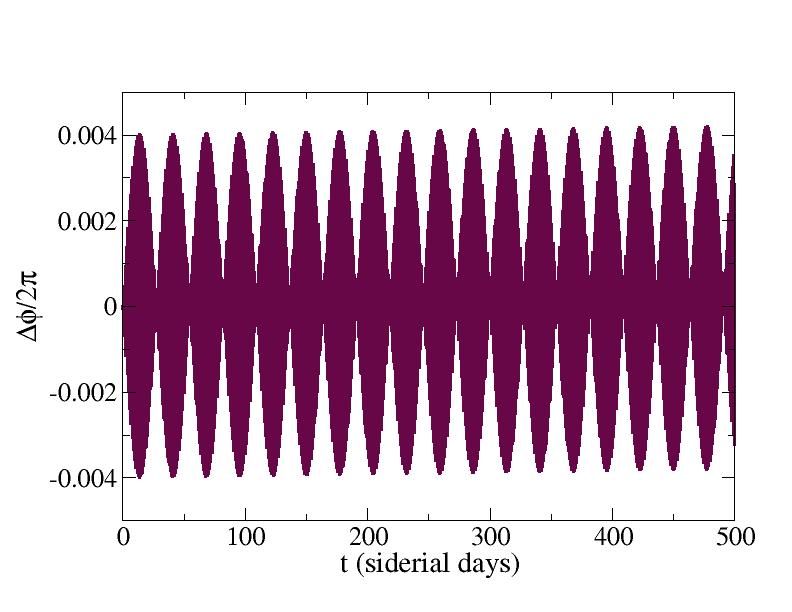
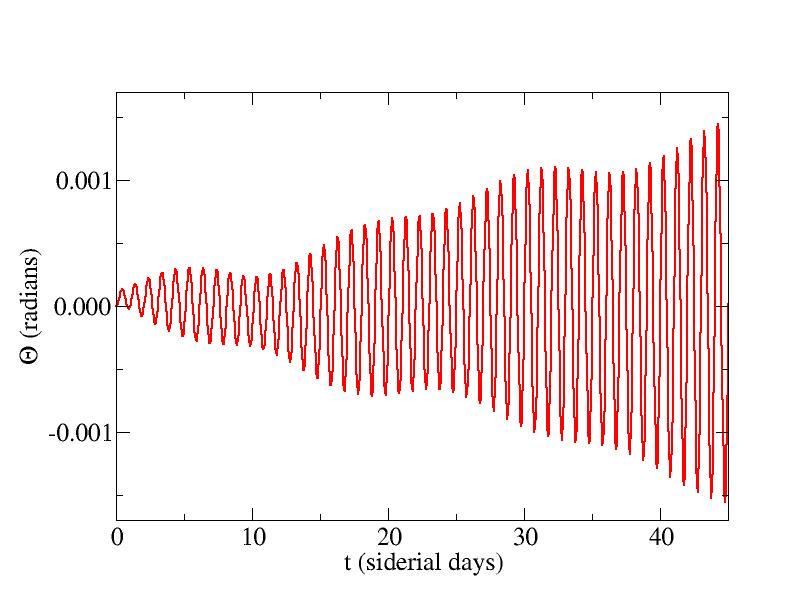
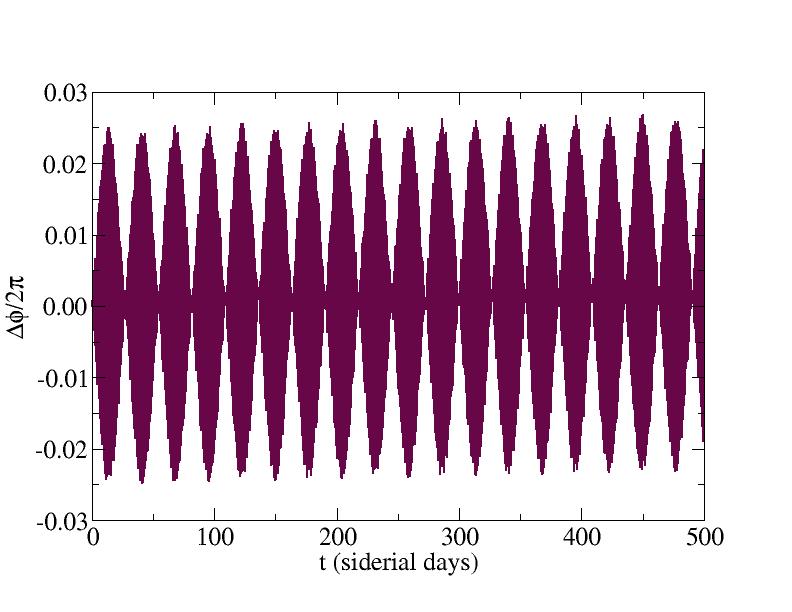
By adjusting the initial period of the orbit (the constant a), we can suppress the overall drift in the angle observed above. By trial and error ("manual bisection"), it is found that T/Ts=1.000486 produces an orbit with no net drift; just oscillations of approximately 1.4 degrees about the stationary position. This may still have to be corrected for in practice because of the high directionality of the transmitted/received radio-frequency signals.
One can understand the main effect of the moon as reducing the effective mass of earth (imagine the mass of the moon beaing spread out uniformly over the orbit). With a reduced mass, the initial orbit has to be higher. This accounts for the over-all drift. The oscillations are clearly beyond this simple approximation.

Problem B (the moon is moving in a 25-degree inclined orbit)

The angular (longitude) deviations are similar to the previous case with an over-all drift and oscillations.
Now the satellite also is pulled outside the equatorial plane, as shown in the following two figures.

Compensating for the drift

As in A, we can compensate for the over-all longitudinal drift by choosing a higher initial orbit. T/Ts=1.000439 gives an orbit with most of the drift removed, as shown in this figure.
However, this does not move the oscillations out of the equatorial plane, as shown in this figure.
Thus we conclude that the moon really ruins the concept of geo-stationary orbit. Sattellites that need to approximate such orbits must therefore be equpped with rockets to allow for occasional adjustments.