Solutions for homework assignment #2

Monte Carlo Integration

F90 solution program [inertia.f90]

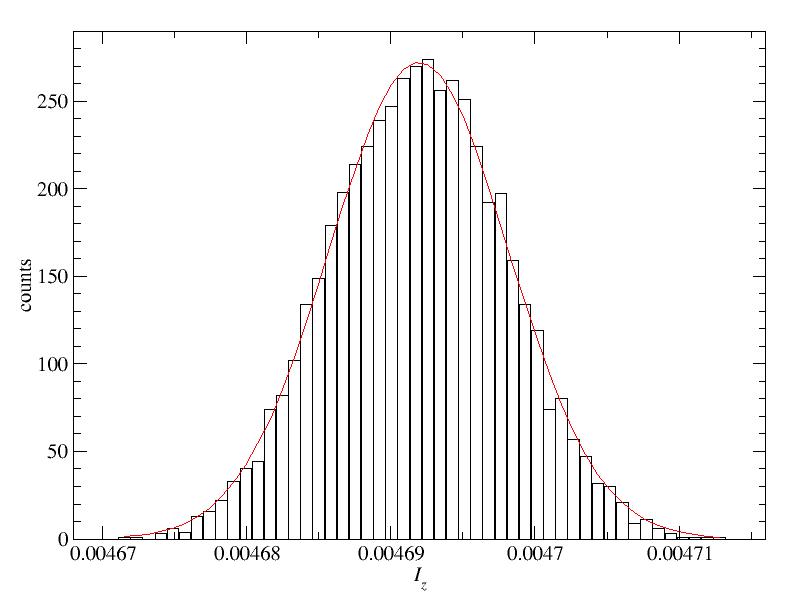
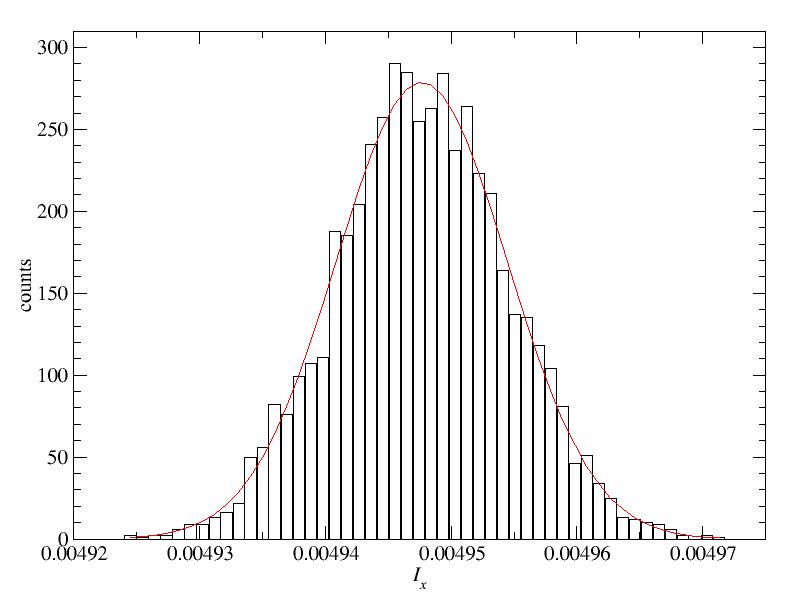
Running the program with 1 million sampling points per bin and nbi bins gave the following results and error bars for Iz and Iy 
  nbi =   50:  Iz = 0.00469302 +/- 0.00000081,  Ix = 0.00494854 +/- 0.00000091
  nbi =  500:  Iz = 0.00469148 +/- 0.00000027,  Ix = 0.00494760 +/- 0.00000031    
  nbi = 5000:  Iz = 0.00469192 +/- 0.00000009,  Ix = 0.00494771 +/- 0.00000010
Note that when increasing the number of bins by a factor of 10, the error bar is reduced approximately by sqrt(10), as expected statistically. The nbi=5000 run gave bin averages with the following distributions (using 50 histogram bins within the range where data appeared):
Gaussians have been fitted to the data sets, demonstrating normal distributions as expected by the central limit theorem when the number of points per bin is large.