Question 14

  Light enters the eye through an opening called the pupil. On the inner side of the pupil is the material from which the eye is made (average index of refraction = 1.36). Suppose, for comparison, that a sheet of opaque material has a hole cut into it. Light passes through this hole into the air on the other side. Assuming that the pupil and the hole have the same diameter, in which case does green light (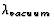$\lambda_{vacuum}$ = 550 nm) diffract more, when it enters the eye or when it passes through the hole in the opaque material? Give your reasoning.

SOLUTION:
Light which enters the eye has its wavelength shortened to

$$\lambda_{eye} = \frac{\lambda_{vacuum}}{n} = \frac{550 nm}{1.36}$$

$$\lambda_{eye} = 404 nm.$$

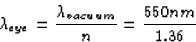
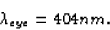
Light which passes through the hole in the sheet still has the same wavelength on the other side, 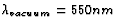$\lambda_{vacuum} = 550 nm$(it's really 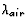$\lambda_{air}$, but that's pretty much the same as 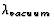$\lambda_{vacuum}$).
Light begins to be diffracted significantly when the size of the hole doing the diffracting becomes comparable to the wavelength of the light being diffracted. Or, as your text puts it, the amount of diffraction depends on the ratio 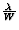$\frac{\lambda}{W}$, where W is the diffracting-hole width. In our problem, the hole width is the same in both cases, but the wavelengths aren't. The wavelength in air is larger than that in the vitreous humor, so the light is diffracted more when it passes through the hole in the sheet.