

Next: Problem 66
Up: Chapter 26
Previous: Problem 47
A camper is trying to start a fire by focusing sunlight onto
a piece of paper. The diameter of the sun is 1.39 x 109 m and
its mean distance from the earth is 1.50 x 1011 m. The camper
is using a converging lens whose focal length is 10.0 cm. (a) What
is the area of the sun's image on the paper? (b) If 0.530 W of
sunlight pass through the lens, what is the intensity of the sunlight
at the paper?
SOLUTION:
(a) The sun is really, really far away (compared to the focal
length of the lens), so using the lens equation with do going to
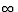 , we see that di is pretty much the same as the focal
length. The magnification is, then,
, we see that di is pretty much the same as the focal
length. The magnification is, then,
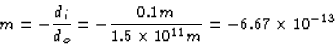
Therefore, the image height is
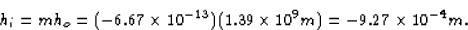
The diameter of the sun's image on the paper is hi. The area of the
image is, therefore,
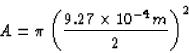
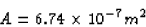
(b) The intensity of the light is the power that strikes the paper
perpendicularly divided by the illuminated area A
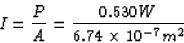
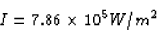


Next: Problem 66
Up: Chapter 26
Previous: Problem 47
Scott Lanning
3/23/1998
![]()
![]()
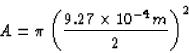
![]()
![]()
![]()