Problem 34

  Suppose that the police car in Example 6 is moving to the right at 27 m/s, while the speeder is coming up from behind at a speed of 39 m/s, both speeds being with respect to the ground. Assume that the electromagnetic wave emitted by the radar gun has a frequency of 8.0 x 10⁹ Hz. (a) Find the magnitude of the difference between the frequency of the emitted wave and the wave that returns to the police car after reflecting from the speeder's car. (b) Which wave has the greater frequency? Why?

SOLUTION:
(a) Call the emitted frequency f = 8 x 10⁹ Hz. The speeder sees the EM wave Doppler shifted to f' different from f. Then the wave reflects off the speeder and bounces back to the police car who observes the reflect wave as having a frequency f'' different than f' at its instant of reflection. When the emitter and observer are approaching each other (as in this case), the magnitude (given in example 6) of the difference in frequency between the emitted wave and the reflected wave is

$$f'' - f \approx 2 f \left ( \frac{u}{c} \right ) .$$

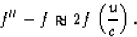
The relative speed u is 39 - 27 = 12 m/s, and c is the speed of light. So,

$$f'' - f \approx 640 Hz .$$

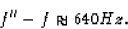
(b) The cars are approaching each other, so the EM waves are ``blue shifted'', that is the Doppler shifted frequency will be greater. (See also equation 24.6 where the plus sign implies that the quantity in brackets will be greater than one.)