

Next: Chapter 29
Up: Chapter 28
Previous: Question 4
In 1992, Jenny Thompson set a world's record for the 100-m
freestyle. Suppose that this race had been monitored from a
spaceship travelling at a speed of 0.8200c relative to the earth
and that the space travellers measured the time interval of the
race to be 95.18 s. What was the time recorded on earth?
SOLUTION:
We are measuring two different events; namely, the start and
finish of the race. We on earth hold the stopwatch in our
hand, so the ticks corresponding to start and finish both
occur at the same point in space. So our measurement of the
time interval is the proper time interval. (You might quibble
that we aren't in the rest frame of the runner-and you'd be
right, of course-but the runner is presumably running at a
velocity with respect to us that is much less than the speed of
light, whereas the space travellers are moving at an appreciable
fraction (0.82) of the speed of light with respect to us, so,
essentially, we are in the same inertial reference frame as the
runner.)
Given the time interval 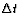 observed by the space
travellers, we can plug into the time dilation formula to get
the time interval on our stopwatch.
observed by the space
travellers, we can plug into the time dilation formula to get
the time interval on our stopwatch.
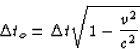
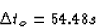


Next: Chapter 29
Up: Chapter 28
Previous: Question 4
Scott Lanning
4/15/1998
![]()
![]()