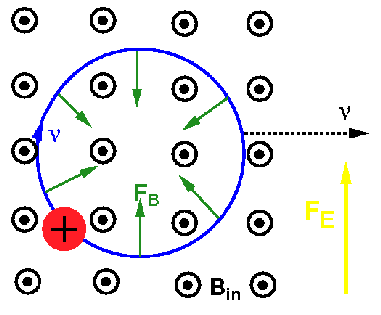
Q16)If a moving charged particle is deflected sideways in some region of space, can we conclude for certain that B is not equal to zero in that region?
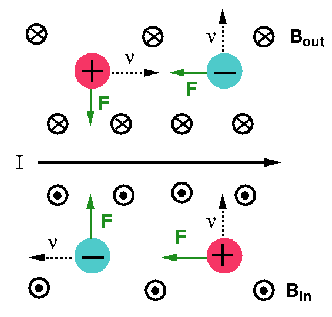
SOLUTION:Q18)In Fig 20-48, charged particles move in the vicinity of a current carrying wire. For each charged particle the arrow indicates the direction of motion of the particle and the + or - indicates the sign of the charge. For each of the particles, indicate the direction of the magnetic force due to the magnetic field produced by the wire.
SOLUTION:

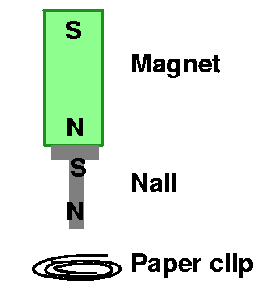
Q29)An unmagnetized nail will not attract an unmagnetized paper clip. However, if one end of the nail is in contact with a magnet, the other end will attract a paper clip. Explain.
SOLUTION:
P49)The Hall effect can be used to measure blood flow rate because the blood contains ions that constitute an electric current. (a)Does the sign of he ions influence the emf? (b)Determine the flow velocity in an artery 3.3mm in diameter if the measured emf is 0.10 mV and B is 0.070 T. (In actual practice, an alternating magnetic field is used.)
SOLUTION:
(a)Positive charge carriers will move up; negative
charge carriers will also move up. Hence the
polarity of the emf
depends on the sign of the charge carrier.
(b)l = 3.3 mm, emf = 0.10 mV, B = 0.20 T
electric field E = vB and (from V = E x d) emf
= (E)(l) = (v)(B)(l)
v = emf / (B)(l) = 0.10 mV / [(0.07 T)(3.3 mm)]
= (10 -4) / [(0.07 T)(3.3 x 10-3 m)] = 0.43
m/s
P50)Protons move in a circle of radius 5.10 cm in a 0.566-T magnetic field. What value of electric field could make their paths straight? In what direction must it point?
SOLUTION:
P54)A mass spectrometer is being used to monitor air pollutants. It is difficult, however, to seperate molecules with nearly equal mass such as CO (28.0106 u) and N2 (28.0134 u). How large a radius of curvature must a spectrometer have if these two molecules are to be seperated on the film by 0.50 mm?
SOLUTION:
In the velocity selector region of the spectrometer E
= v B
In the mass spectrometer region, the
force with which the particle forms a curved path is:
mv2 / r = q vB'
so, r = mv / q B' = m E / (q B B') and the radius of the curve is
proportional to the mass of the particle.
For the
two species to be separated by (delta r) = 0.50 mm,
we need (delta r) = (delta m) E / q B B'
= (delta m) (r / m),
so r = m (delta r) / (delta m) = (28.012
u)(0.5 mm) / (0.0028u) = 5.0 m
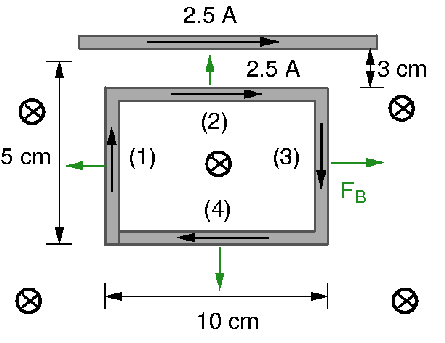
P58)A rectangular loop of wire is sitting next to a straight wire, as shown in Fig. 20-59. There is a current of 2.5 A in both wires. What is th magnitude and direction of the net force on the loop?
SOLUTION:
P63)A doubly charged helium aton, whose mass is 6.6 x 10-27 kg, is accelerated by a voltage of 2400 V. (a)What will be its radius of curvature in a uniform 0.240-T field? (b)What is its period of revolution?
SOLUTION: