Homework 5

Chapter 19

P52)In Fig. 19-17a, the total resistance is 15 ohms, and the battery emf is 24.0 V. If the time constant is measured to be 35 µs, calculate (a) the total capacitance of the circuit and the (b) the time it takes for the voltage across the resistor to reach 16.0 V.

SOLUTION:
   (a)Since we know the time constant tau = R C =35 µs
   C = 35 x 10-6 / 15000 ohms = 2.33 x 10-9 F
   (b)current = Ioe-t / RC, Io = 24 V / 15000 ohms = 1.6 mA
   Voltage across the resistor is V = Io(15 kohms)e-t / RC = (24 V) e-t / 35 µs
   V = 16 if 16 = 24 e-t / 35 µs
   e-t / 35 µs = 1.5, t / 35 µs = ln(1.5), t = (35 µs) ln(1.5) = 14.2 µs

P57)A galvanometer has an internal resistance of 30 ohms and deflects full scale for a 50-µA current. Describe how to use this galvanometer to make (a) an ammeter to read currents up to 30 A, and (b) a voltmeter to give a full-scale deflection of 1000 V.

SOLUTION:
   (a)We neet a shunt resistor, so that the ammeter has a maximum deflection when the current down the    shunt is I = 50-µA. The rest of the current goes down the parrallel path with resistor R.
   so, (30 A) (R) = (50 x 10 -6) (r) where r = 30 ohms.
   R = (50 / 30) x 10 -6 x 30 ohms = 50 x 10 -6 ohms.
   (b)We need a series resistance, so that the total voltage across both resistor R + r is 1000 V
   so, 50 x 10 -6 (R + r) = 1000 ohms.
   R + r = 20 µ-ohms and since r << R, R = 20 µ-ohms

P69)A three-way lightbulb can produce 50W, 100W, or 150W, at 120 V. Such a bulb contains two filaments that can be connected to the 120 V individually of in parallel. Describe how the connections to the two filaments are made to give each of the three wattages. What must be the resistance of each filament?

SOLUTION:
   P1 = (120 V)2 / R1 = 50 W so, R1 = 288 ohms.
   P2 = (120 V)2 / R2 = 100 W so, R2 = 144 ohms
   P3 = (120 V)2 / (1 / R1 + 1 / R2) = 150 W so,
.

Chapter 20

Q3)In what direction are the magnetic field lines surrounding a straight wire carrying a current that is moving directly toward you?

SOLUTION:


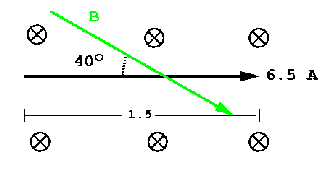
P2)A 1.5-m length of wire carrying 6.5 A of current is oriented horizontally. At that point on the Earth's surfance, the dip angle of the Earth's magnetic field makes an angle of 40o to the wire. Estimate the magnetic force on the wire due to the Earth's magnetic field of 5.5 x 10 -5 T at this point.

SOLUTION:


   | F | = (I) (L) (| B |) sin(40o) = (6.5) (1.5) (5.5 x 10 -5 ) (0.643) N
   | F | = 3.45 x 10 -4 N, force is into paper.

P9)Alpha particles of charge q = +2e and mass m = 6.6 x 10-27kg are emitted from a radioactive source at a speed of 1.6 x 10 -7 m/s. What magnetic field strength would be required to bend these into a circular path of radius r = 0.25m?

SOLUTION:
   Force = m acent = m v2 / r = q v B
   B = (m v) / (q v) = (6.6 x 10-27kg)(1.6 x 107 m/s) / [(3.2 x 10-19C) (0.25 m)]
   B = 1.32 T

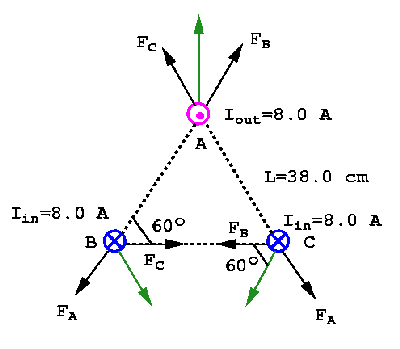
P31)Three long parallel wires are 38.0 cm form one another. (Looking along them, they are at three corners of an equilatieral triangle.) The current in each wire is 8.00 A, but that in wire A is opposite to that in wires B and C (Fig. 20-54). Determin the magnetic force per unit length on each wire due to the other two.

SOLUTION:


   (a) | Ftot | on A due to B and C:
   | F 2 | / L = | F 3 | / L = [µo I1 I2] / [2 (pi) r] = force / length
   | F 2 | / L = (2 x 10 -7)(8)(8) / (0.38) N/m = 3.37 x 10 -5 N/m
   Ftot on A points up, since the sideways components cancel.
   | Ftot| = 2 | F2 | cos(30o = 5.84 x 10-5 N
   (b) | Ftot | on B due to A and C:
   By symmetry, | Ftot | is 60o below the line connecting B and C
   | F tot | / L = (| Ftot |y / L) sin(60o) / L
   | F tot | / L = 3.4 x 10-5 N/m
   (c)similarly, the force on C is 60o below the line going from C and B,
   | F tot| / L = 3.4 x 10-5 N/m

P36)A 30.0-cm long solenoid 1.25 cm in diameter is to produce a field of 0.385 T at its center. How much current should the solenoid carry if it has 1000 turns of the wire?

SOLUTION:
   B = µo (N / L) I
   I = (B L) / (µo N) = (0.385) (0.30) / [(4 pi x 10-7) (1000)]
   I = 92.0 A

BU CAS PY 106
This page maintained by Anna Skibinsky
askibins@buphy.bu.edu