Homework 4

Chapter 18

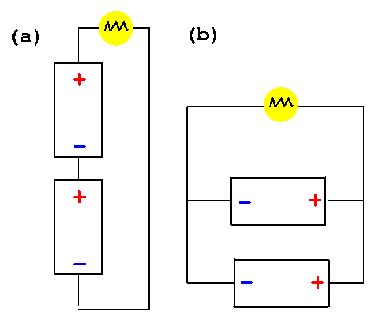
Q15)Some lamps might have batteries connected in either of the two arrangements shown in Fig.18-30. What would be the advantages of each scheme?

SOLUTION:


Arrangement (a) provides greater voltage across the filament, making the bulb shine more brightly. Arrangement (b) permits the bulb to burn a longer because each battery provides less current than the batteries in (a).

P31)An ordinary flashlight uses 2 D-cell batteries (1.5 V each) and draws 350 mA when turned on. (a) Calculate the resistance of the bulb and the power dissipated. (b) By what factor would the power increase if 4 D-cells in series were used with the same bulb? (Neglect the heating effects of the filament.) Why shouldn't you try this?

SOLUTION:
   (a) V = I x R
   R = 2 x 1.5-V / 0.35 A = 8.6 ohms
   P = V2 / R = 92/ R = (9-V2) / (8.6 ohms) = 1.05 W
   (b) Power would increase by a factor of 4. Using 4-cells would thus, not be a good idea since the bulb will
   probably burn out.

P46)A heater coil connected to a 240-V ac line has a resistance of 34 ohms. What is the average power used? What are the maximum and minimum values of the instantaneous power?

SOLUTION:
    Pave = V2rms / R = average power.
    Vrms = 240-V so Pave = (240-V)2 / (34) W = 1700 W
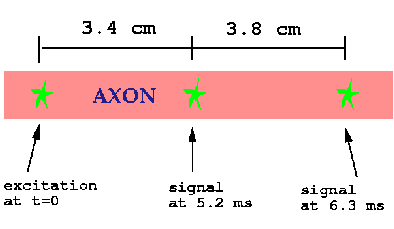
    Pmax = V2max / R = [(2)1/2 Vrms]2 / R = 3400 W.
    Pmin = 0

P52)A nerve is stimulated with an electric pulse. The action potential is detected at a point 3.40 cm down the axon 0.0052 s later. When the action potential is detected 7.20 cm from the point of stimulation, the time required is 0.0063 s. What is the speed of the electric pulse along the axon? (Why are two measurements needed instead of only one?)

SOLUTION:


There are several ways one might calculate transmission speed:    v1 = 3.4 cm / 5.2 ms = 6.5 m/s
   v2 = (3.4 cm + 3.8 / 6.3 ms = 11.4 m/s
   v3 = 3.8 cm / 1.1 ms = 34.5 m/s
If one assumes the speed is the same at all points in the axon (a good assumption), the difference of v1 and v3 suggests the excitation does not produce a nerve signal immediately. Hence, one must use v3

Chapter 19

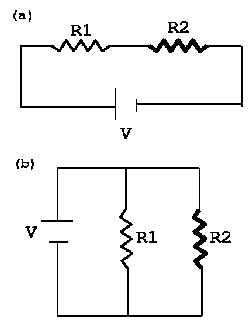
Q4)Two lightbulbs of resistance R1 and R2 (> R1) are connected in series. Which is brighter? What if they are connected in parallel?

SOLUTION:


    (a) I = V / (R1 + R2)
    P1 = I2 R1 and P2 = I2 R2
    since R2 > R1,    P2 > P1 and bulb 2 is brighter.
    (b) P1 = V2 / R1 and P2 = V2 / R2
    so in this case, since R2 > R1,    P2 < P1 and bulb 1 is brighter.

P22)What is the internal resistance of a 12.0-V car battery whose terminal voltage drops to 8.8 V when the starter draws 60 A? What is the resistance of the starter?

SOLUTION:
    R = starter resistance and r = battery internal resistance
    voltage drop across resitor r is 3.2 V =(I x r) so r = (3.2 / 60) ohms = 0.053 ohms
    (r + R) = 12 V / 60 A so R = 0.2 ohms - 0.053 ohms = 0.147 ohms.

P24)Calculate the current in the circuit of Fig. 19-36 and show that the sum of all the voltage changes around the circuit is zero.

SOLUTION:
    9.0 V = I (2.0 ohms + 8 ohms + 2 ohms)     I = (9 / 22) A = 0.41 A

    Vnet = 9.0V - 0.41 (2.0 ohms) - 0.41 (8 ohms) - 0.41 (2 ohms) = 0

P28)Determine the magnitudes and directions of the currents through R1 and R2 in Fig 19-37.

SOLUTION: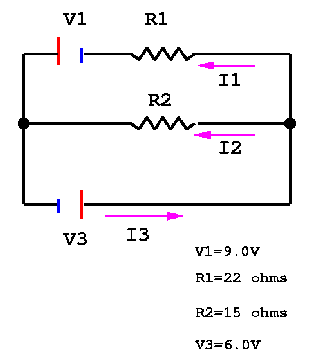
    For the loop containing V1, R1, V3,
    sum of the voltage sources is 9.0 V + 6.0 V = 15 V. The sum of the voltage drop is I1 R1 so,
    15 V = I1 R1    and    I1 = 0.68 A
    For the bottom loop,
    6.0 V = I2R2,    I2 = 0.4 A

BU CAS PY 106
This page maintained by Anna Skibinsky
askibins@buphy.bu.edu